推定統計学では
研究者、実験者が
考えた仮説に対し
データから統計的に
証明する手法
仮説検定という手法があります
今回は検定の基本的な
考え方について
説明します
[PR]※本サイトにはプロモーションが含まれています
検定の考え方

私は賢いタコ
サッカーの
試合の
勝敗を予言する
能力を持っています
なのでタコ焼きに
して食べないで
ください

すごい!
このタコは予言能力を持っていると
いえるだろうか?
ある学者Aはこう主張します

タコの勝敗予言能力は
根拠がないので
能力はないと
考えます
この学者Aの主張のように
何かが「ない」ことを示す仮説を
帰無仮説 \(H_0\)と言います
\(H_0\):タコは勝敗予言能力が「ない」
言い換えますと
\(H_0\):タコは適当に勝敗を予想している
帰無仮説を立てる
先ほど下記のように帰無仮説を立てました
\(H_0\):タコは適当に勝敗を予想している
勝敗は勝ち負けの2つの結果のみです
適当に予想すれば当たることもあるし
外れることもあります
帰無仮説の元勝敗予想は
成功確率 \(\displaystyle = \frac{1}{2}\)
のベルヌーイ試行を行っていると考えられる
帰無仮説の妥当性を評価する
帰無仮説の元で
n回中x回予想が当たる確率は
二項分布を用いて
\(\displaystyle P(x❘H_0)=nC_x(1/2)^n\)で
求められる
20回の試行で的中する確率は\(\displaystyle \frac{1}{2^{20}}\)
この確率は凄く小さい
区別がついていたように思われる
このように帰無仮説の元で発生する確率が
小さい事象が確認された場合
確率が小さい事象が偶然起こったのではなく
帰無仮説は正しくないと考える

20回すべて
勝敗予想を当てました

20回すべて
当たる確率は
約\(9.54×10^{-7}\)
これは偶然じゃない!
検定の基本的な構造
タコが20試合中14試合の結果を
的中させた
帰無仮説の元この確率は
\(20C_{14}(1/2)^{14}= 0.037\)
適当に勝敗予想していた場合
的中させる期待値は
x = 10 である
タコは14回予想を的中させたので
期待値から4離れている
これを珍しい結果と考えると
確率変数が期待値から4以上離れている値になるのは
更に珍しいと仮説を立てる
確率変数は二項分布に従うので
期待値から4以上離れる確率変数になる確率は
\((P(❘x-μ❘ ≧ 4 ❘ H_0)≒0.115\)
11.5%なのでそれほど珍しい現象ではない
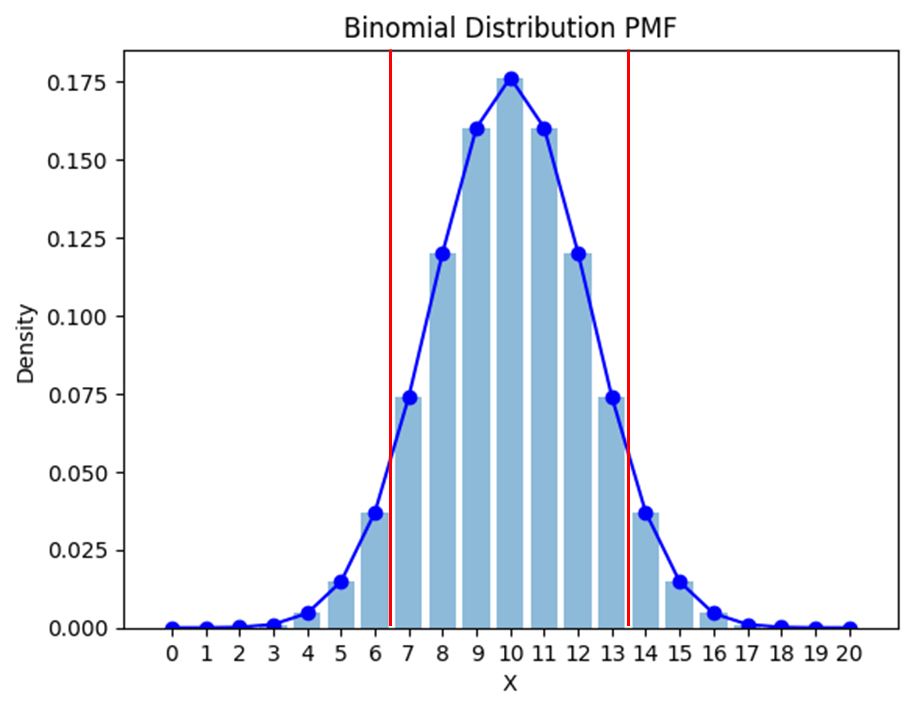
帰無仮説で建てられる確率分布の裾を
基準とし基準となる値α(有意水準)
より小さい時に帰無仮説は
棄却され正しくないと判定するのが
統計的仮説検定の基本的な考え方である
有意水準α = 0.05とすると
\((P(❘x-μ❘ ≧ 4 ❘ H_0)≒0.115\)より
有意水準より大きいので
タコは試合の勝敗を予想する能力を
持っていないと判断する

・・・

・・

・・・
参考文献

日本統計学会公式認定
統計検定2級対応
統計学基礎

4章:統計的仮説検定
仮説検定の考え方より