
今回は
ベルヌーイ分布
二項分布
に関して紹介します
[PR]※本サイトにはプロモーションが含まれています
目次
ベルヌーイ分布
ベルヌーイ分布とは、
離散確率分布の一種であり
成功(成功確率 p)と失敗(失敗確率 1−p)
の二つの結果しか持たない試行の確率分布です

結果が2パターン
しかないのか~!
\(P(X=K)=P^k(1-P)^{1-k}\)
k:0 もしくは1
P:1回の試行でK = 0か1の結果が出る確率
期待値と分散は
\(E[X] = μ = p \)
\(V[x] = E[x] – μ^2 = p(1-p)\)
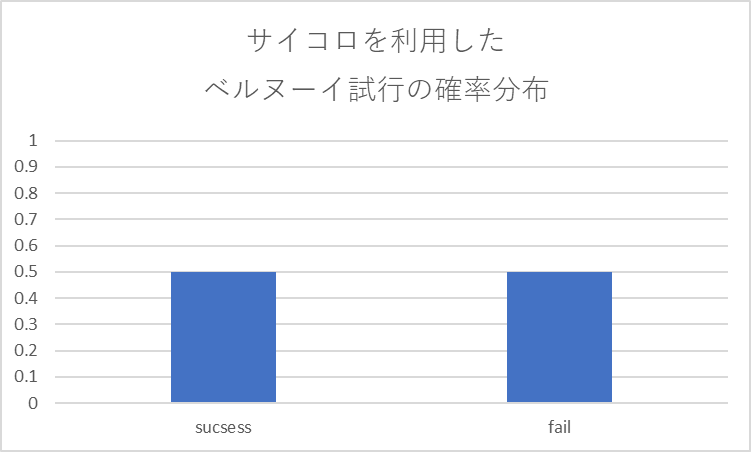
サイコロを利用したベルヌーイ試行の結果の確率分布
サイコロを投げて
偶数が出た場合を成功
奇数が出た場合を失敗とすると
失敗か成功かしか結果がないので
この試行はベルヌーイ試行です
ベルヌーイ試行の結果を
0(失敗)と1(成功)とし
成功確率をPとすると
\(P(X=1)=\frac{1}{2}\)
\(P(X=0)=\frac{1}{2}\)
確率分布は

成功か失敗か
単純な
離散確率分布
なんだね~
Pythonを使ってベルヌーイ分布の確率密度関数の値を出力するコードを実装
ある実験を繰り返し10回行った所8回成功し2回失敗した。
成功=1失敗=0とし
表にまとめるとこのようになった。
[0,0,1,1,1,1,1,1,1,1]
\(P(x=0)\),\(P(x=1)\)を求めよ
import numpy as np
import matplotlib.pyplot as plt
# ベルヌーイ分布
# fail:0,sucsess:1
prob_data = np.array([])
data = np.array([0,0,1,1,1,1,1,1,1,1])
for i in np.unique(data):
P = len(data[data==i])/len(data)
print(i,"が出る確率",P)
prob_data = np.append(prob_data,P)
print(prob_data)
plt.bar([0,1],prob_data,align = 'center')
plt.xticks([0,1],['fail','sucsess'])
plt.grid(True)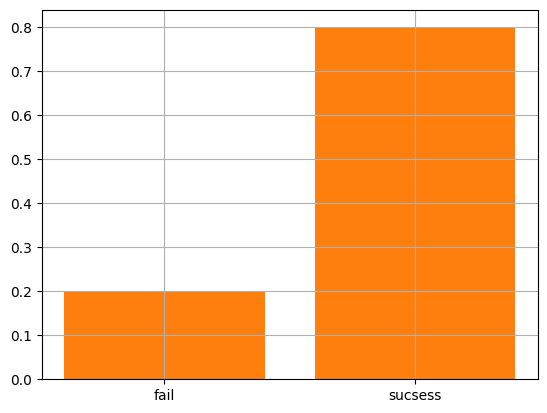
二項分布
成功確率を p
失敗確率を 1−p とすると
n回 のベルヌーイ試行を行った際に
n 回の試行のうち特定の x 回で成功し
残りの n−x 回失敗する
この確率を計算し
全ての確率変数の確率を
棒グラフに分布化したものが
二項分布です。
\(P(X=x)=nC_x・P^x・(1-P)^{n-x}\)
期待値
\(E[X]=np\)
分散
\(V[X]=np(1-P)\)

二項分布は
ベルヌーイ分布を
複数回やって
何回成功するか
失敗するかの
確率を表す
分布なんだね!
【例題3】コイン投げ
コインを10回投げたとき3回表が出る確率を
二項分布を利用して求めよ
コインを10回投げたとき3回表が出る事象の数
\(10C_3\)より
\(=120\)

10回コインを投げて
7回裏、3回表が
出る組み合わせは
120通りあるんだね!
表が出る回数は3回
\(x=3\)
表が出る確率Pは
\(\displaystyle P=\frac{1}{2}\)
二項分布の公式より
10回中3回コインが表が出る確率は
\(\displaystyle P(X=3)=10C_3・(\frac {1}{2})^3・(\frac {1}{2})^7\)
\(=0.117\)
Pythonで二項分布の実験をしてみる
コインを10回投げて
表が出る回数Xを確率変数とし
確率変数Xを0~10まで全ての
確率を求めて棒グラフを作成し
確率分布を作成せよ
from scipy.stats import binom
import matplotlib.pyplot as plt
import numpy as np
# パラメータの設定
p = 0.5 # 成功確率
n = 10 # 試行回数
# 二項分布
x = np.arange(0, n+1)
pmf = binom.pmf(x, n, p)
# 結果の表示
print(f'試行回数: {n}, 成功確率: {p}')
print(f'確率密度関数 (PMF): {pmf}')
# グラフの描画
plt.bar(x, pmf, align='center', alpha=0.5)
plt.plot(x, pmf, marker='o', linestyle='-', color='blue', label='PMF Line')
plt.title('Binomial Distribution PMF')
plt.xlabel('X')
plt.ylabel('Density')
plt.xticks(x, x)
plt.show()
print('確率密度関数の総和',sum(pmf))出力結果の値は
| 事象 | 確率密度関数 | 値 |
| 表が一回も出ない | \(P(X=0)\) | 0.00097656 |
| 表が1回出る | \(P(X=1)\) | 0.00976563 |
| 表が2回出る | \(P(X=2)\) | 0.04394531 |
| 表が3回出る | \(P(X=3)\) | 0.1171875 |
| 表が4回出る | \(P(X=4)\) | 0.20507812 |
| 表が5回出る | \(P(X=5)\) | 0.24609375 |
| 表が6回出る | \(P(X=6)\) | 0.20507812 |
| 表が7回出る | \(P(X=7)\) | 0.1171875 |
| 表が8回出る | \(P(X=8)\) | 0.04394531 |
| 表が9回出る | \(P(X=9)\) | 0.00976563 |
| 表が10回出る | \(P(X=10)\) | 0.00097656 |
グラフの出力結果は
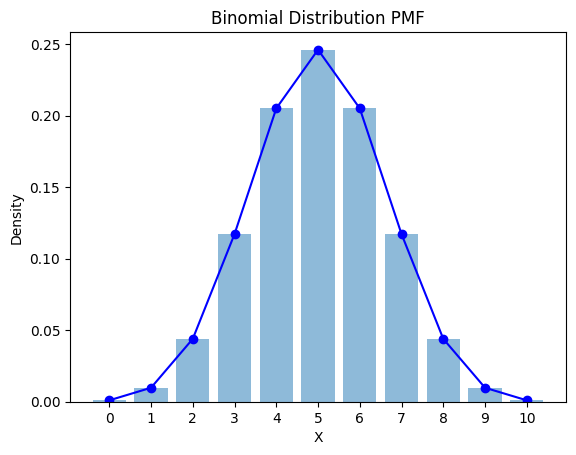

確率が50%なので
確率的に10回コインを振った時
5回表が出る確率が
一番高いんですね!
この実験で
一番期待できる値は5です


