Rを使ってロジスティック回帰を実装する

Yamu

今回はRを使って
ロジスティック回帰を実装
その後指標を確認して
モデルを評価します

[PR]※本サイトにはプロモーションが含まれています

合わせて読みたい

【回帰分析】色々なデータをロジスティック回帰モデルに当てはめてみる

【回帰分析】ロジスティック回帰モデルとは ?糖尿病の疾患と血糖値のデータでモデル化して説明する

1 今回使うデータセット
2 Rでロジスティック回帰モデルを実装する

今回使うデータセット

1.殺虫剤の濃度と死亡率

殺虫剤の濃度 x	0.4	0.57	0.7	0.8	1
虫の数	51	48	46	49	50
死亡数	6	16	24	42	44
死亡率	0.12	0.33	0.522	0.857	0.88

表1 :殺虫剤の濃度と死亡率

下記コードをrに書き込みデータセットします

# 濃度
x = c(0.4, 0.57, 0.7, 0.8, 1)

# 虫の数
m = c(51, 48, 46, 49, 50)

# 死亡数
y = c(6, 16, 24, 42, 44)

# 死亡率
p = y/m

# データフレームの作成
data = data.frame(x, m, y, p)

# データフレームの表示
print(data)

実行結果

     x  m  y         p
1 0.40 51  6 0.1176471
2 0.57 48 16 0.3333333
3 0.70 46 24 0.5217391
4 0.80 49 42 0.8571429
5 1.00 50 44 0.8800000

Rでロジスティック回帰モデルを実装する

殺虫剤の強さ(濃度)と

死亡率を散布図に

プロットするコードを書きます

plot(x, p, xlim =c(0,1.2), ylim =c(0, 1), pch =19, cex =1.5, cex.lab =1.5)

実行結果

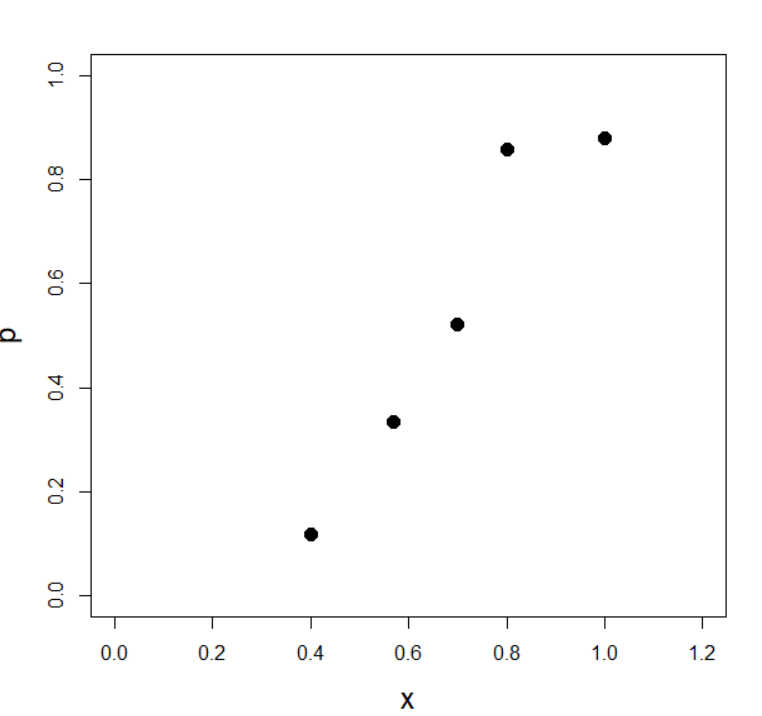
plotのオプションの説明をします

オプション	コードの意味
plot(x,y)	2つのベクトルをプロット
xlim	x軸の範囲
ylim	y軸の範囲
pch	プロットの形状を示す
cex	プロットするサイズ
cex.lab	x軸とy軸のラベルのサイズを指定

ロジスティック回帰分析を行う

コードを紹介します

res = glm(cbind(y, m - y) ~ x, family = "binomial", data = data)
res

cbind(y, m -y)によって

二項分布における成功と失敗のペアを持つ行列が生成されます

ここでいう成功と失敗は

虫の死亡数と生存数です

family = “binomial”で回帰モデルを生成します

実行結果

Call:  glm(formula = cbind(y, m - y) ~ x, family = "binomial", data = data)

Coefficients:
(Intercept)            x  
     -4.940        7.497  

Degrees of Freedom: 4 Total (i.e. Null);  3 Residual
Null Deviance:      98 
Residual Deviance: 5.881        AIC: 29.1

Coeffocoentsに回帰係数

Null Devianceに最大逸脱度

Residual Devianceに残差逸脱度

一般的に、モデルの適合度が良い場合

Residual Deviance は Null Deviance

よりもかなり小さい値になります

Null Deviance と Residual Deviance の差が大きいほど

予測変数が応答変数をうまく説明していることを示しています。

このモデルはResidual Devianceがとても小さい値になっているので

予測変数 x が応答変数 y を

非常によく説明していることを示しています

ロジスティック回帰をプロットします

x_seq <- seq(min(data$x), max(data$x), length.out = 100)
y_pred <- predict(res, newdata = data.frame(x = x_seq), type = "response")
lines(x_seq, y_pred, col = "red", lwd = 2)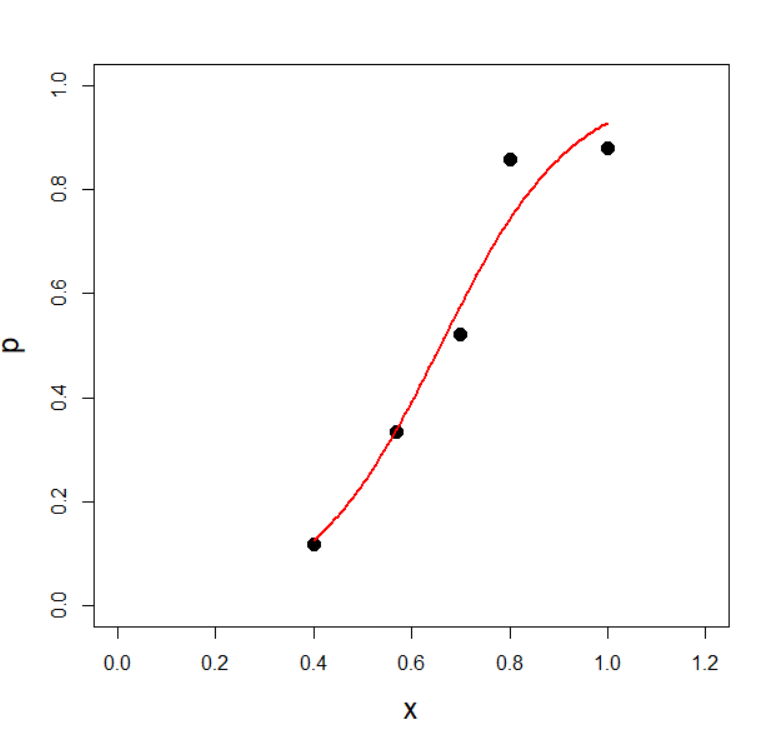

最後にコードを纏めておきます

# 濃度
x = c(0.4, 0.57, 0.7, 0.8, 1)

# 虫の数
m = c(51, 48, 46, 49, 50)

# 死亡数
y = c(6, 16, 24, 42, 44)

# 死亡率
p = y/m

# データフレームの作成
data = data.frame(x, m, y, p)

# データフレームの表示
print(data)

plot(x, p, xlim =c(0,1.2), ylim =c(0, 1), pch =19, cex =1.5, cex.lab =1.5)

res = glm(cbind(y, m - y) ~ x, family = "binomial", data = data)
res

x_seq <- seq(min(data$x), max(data$x), length.out = 100)
y_pred <- predict(res, newdata = data.frame(x = x_seq), type = "response")
lines(x_seq, y_pred, col = "red", lwd = 2)