今回は
工程能力指数
CpやCpkについて
解説していきます
[PR]※本サイトにはプロモーションが含まれています
目次
工程能力指数(Process Capability Index, PCI)とは?
製造プロセスのパフォーマンスを
評価するための統計的指標であり
製品が規格内に収まる能力を示します
主に以下の2つの指数がよく使われます: \(C_pとC_{pk}\)

どんな指標なんだろう?
\(Cp\)(能力指数)と\(C_{pk}\)(性能指数)
計算式を纏めてみました
| 記号 | 計算式 | 計算式の意味 |
| \(C_p\) | \(\displaystyle \frac{USL-LSL}{6σ}\) | 上限規格と下限規格の製品仕様範囲と製品の正規分布6σの範囲の比率を示します |
| \(C_{pk}\) | \(\displaystyle \frac{μ-LSL}{3σ}\) | 分布の中心から製品仕様の下側規格の差と3σの範囲の比率を示します |
| \(C_{pk}\) | \(\displaystyle \frac{USL-μ}{3σ}\) | 製品仕様の上側規格と分布の中心の差と3σの比率の範囲を示します |
LSL (Lower Specification Limit): 下限規格値
σ: プロセスの標準偏差

能力指数の計算式は
σがあるので
統計学の確率分布
に基づいた指標
なんだね!
何故工程能力指数に確率分布の考え方が応用されているか
工場でモノを作っているとき
工程が安定状態の時製品の特性データは正規分布に
従うと考えられているからです
ある工程でどんなに正確にモノを
作ったとしても製品の特性
大きさに関してばらつきが生じる
そして工程が安定状態の時
作ったモノの値を
無限回測定し確率分布を確認すると
正規分布になる
つまり測定値が従う確率分布は
「正規分布」になります
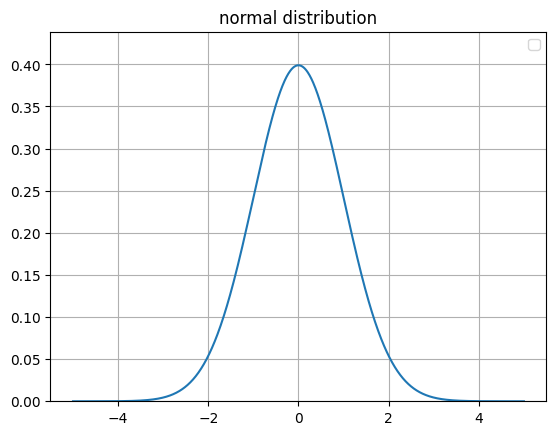
製品の特性データが正規分布に従わない時
規格に沿った製品が作れていないということなので
工程に何らかの異常が発生していると考えられます。
エンピリカルルール
正規分布では
データの約68%が平均から
±1標準偏差の範囲内に
約95%が±2標準偏差の範囲内に
約99.7%が±3標準偏差の範囲内に存在します。
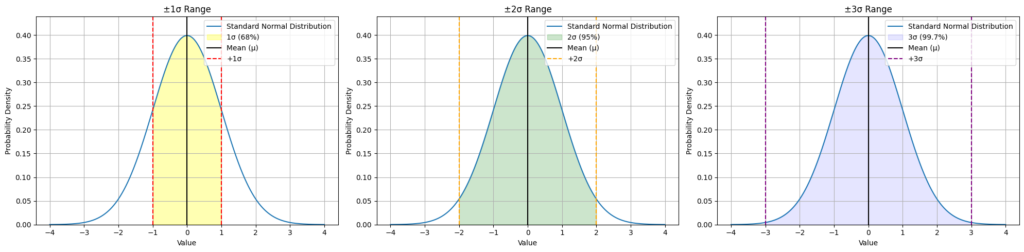

工程能力指数は
このエンピリカル
ルールを利用して
計算されます
Cp(能力指数)
この指数は、プロセスがどれだけ幅広い範囲にわたって
製品を作ることができるかを示します
\(\displaystyle C_p = \frac{USL-LSL}{6σ}\)
\(C_p=1\)の時
\((USL-LSL)=±3σ\)
つまり\(C_p=1\)の時
6σの幅と製品の両側規格の幅が
同じということを示します。
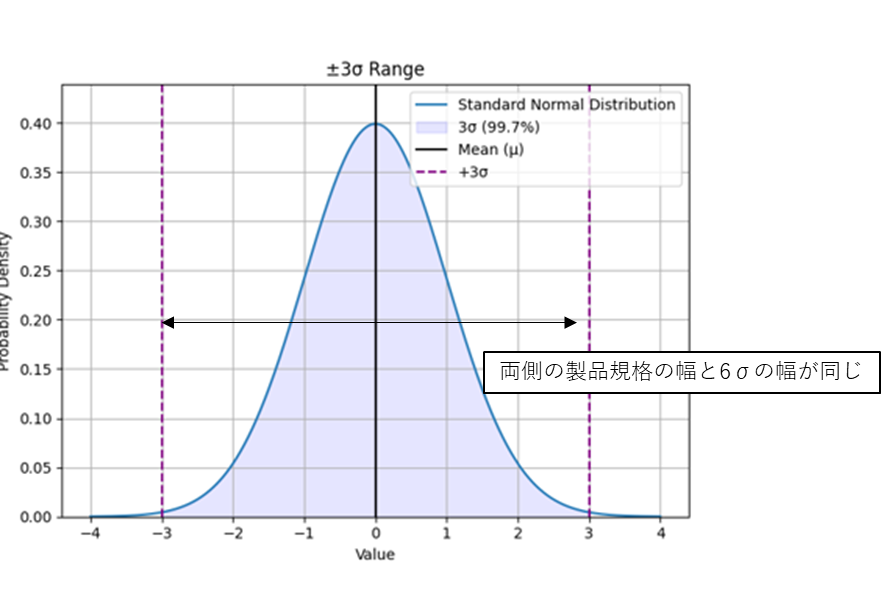
あるプロセスで作られた製品は
上限規格と下限規格の製品仕様範囲から
0.03%の確率で外れるということを示しています
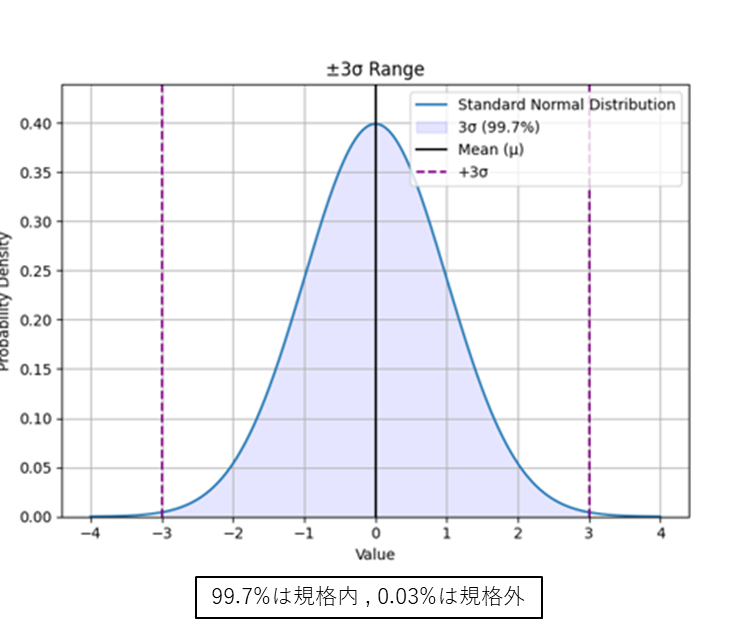
これを現実に起こっていることに換算すると
ある工場の工程で1000個モノを作ったら3個規格外の製品が
できますよーといった感じです。
一般的には\(C_p=1.33\)で工程能力は十分である
といった判断をします。
Cpが1.33なら
USL-LSL = ±3σ×1.33
±4σ(99.994%)
つまり、Cp = 1.33の能力をもった工程で
製品を作った時
10万個に6個しか規格外の製品は発生しないはずです
工程能力指数で工程能力の評価
| \(\displaystyle C_p≧1.33\) | 工程能力は十分である |
| \(\displaystyle 1.33>C_p≧1.00\) | 工程能力はほぼ良好である |
| \(1.00>C_p\) | 工程能力は不足している |
Cpk (性能指数)
プロセスの平均値が片側規格の値と
どれだけずれているかを考慮し
プロセスが規格内に収まる能力を示します
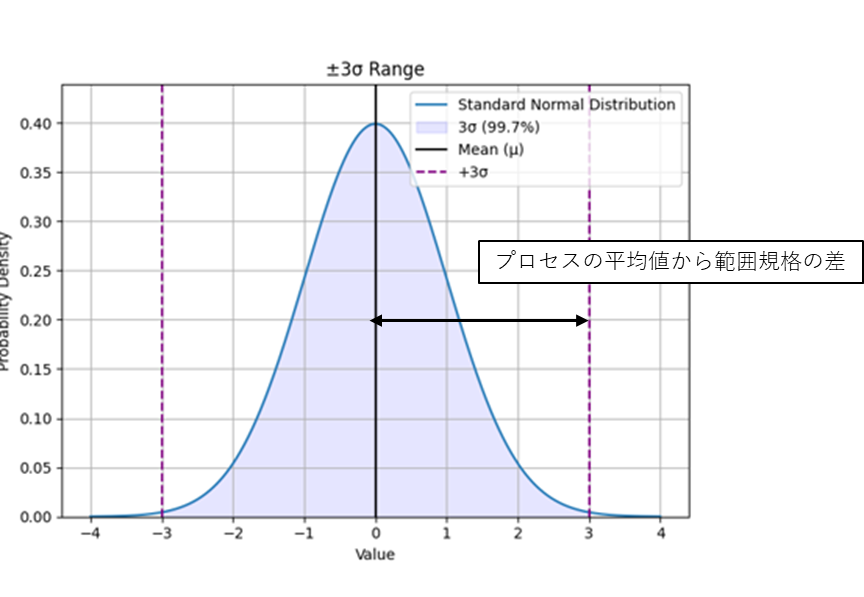
上限規格
\(\displaystyle \frac{S_U-μ}{3σ}=\frac{上限規格-平均値}{3σの範囲}\)
上限規格と分布の中心(平均値)の差と
製品の正規分布の3σの比率を示します。
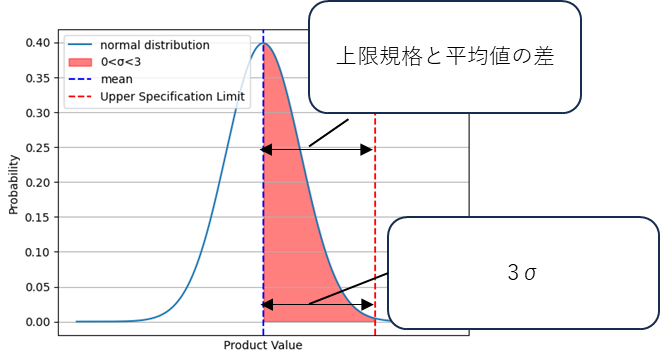
指標の評価を纏めるとこんな感じです。
下限規格のみある場合
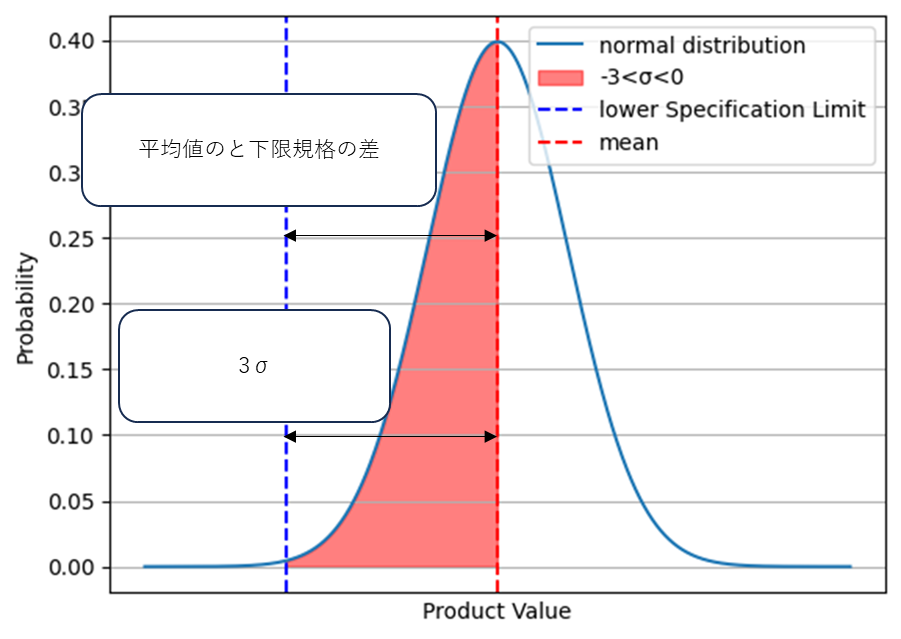
\(\displaystyle \frac{μ-S_L}{3σ}=\frac{平均値-下限規格}{3σの範囲}\)
分布の中心と下限規格の(平均値)の差と
製品の正規分布の3σの比率を示します。
指標の評価を纏めるとこんな感じです。
| \(\displaystyle C_{pk}≧1.33\) | 工程能力は十分である |
| \(\displaystyle 1.33>C_{pk}≧1.00\) | 工程能力はほぼ良好である |
| \(1.00>C_{pk}\) | 工程能力は不足している |
上限規格と下限規格両方ある場合
\(C_{pk}\)が低い方がスペックの
特性が悪いということなので
低い方を選択します