今回は
点推定と区間推定の
について説明致します
[PR]※本サイトにはプロモーションが含まれています
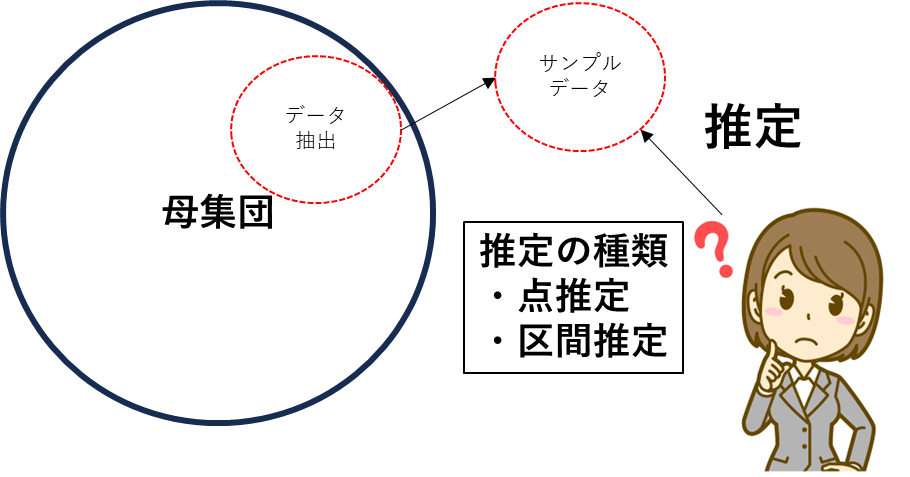
推定とは
サンプルデータから
未知のパラメータや母集団の特徴を
予測する手法として
推定といった手法があります!
推定の種類は
点推定、区間推定です
点推定と区間推定の違い
点推定と区間推定について
表に纏めてみました。
| 推定 | 推定方法 |
| 点推定 | 1つの値(推定値)から母集団のパラメータを推定する |
| 区間推定 | サンプルデータから二つの値を計算しその中に母集団のパラメータが含まれるという表現を用いて推定する |

今回は
点推定は1点
区間推定は区間
点推定(Point estimation)
点推定とは
母集団のパラメータ未知数θ(シータ)の値を
データから計算された一点の推定値
から推定する手法のことを言います
推定値を\( \hat θ\)といった記号で表すのが
一般的です
| 不偏推定量 | 意味 |
| \(E(\hat θ)=θ\) | データから計算された推定値の期待値は母数の値になる |
| \(E(\bar x)=μ\) | データから計算された平均値の期待値は母数の値になる |
| \(E((V)=σ^2\) | データから計算された不偏分散の期待値は母数の値になる |
点推定の計算
以下のようなデータがある
データから母平均の推定値を求めよ
| No | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| データ | 10 | 10.5 | 9.5 | 12 | 9 | 7 | 8.5 | 12 | 14 | 12 |
1.データの異常値をチェックする

異常値はなさそ!
2.平均値を計算する
\(\bar x=\frac{10+10.5+9.5+12+9+7+8.5+12+14+12}{10}\)
\(\bar x=10.45\)
\(E(\bar x)=μ\) より
母平均μの推定値は\(\bar μ=10.45\)
母平均μの点推定は\(\bar μ=10.45\)
区間推定
標本から二つの値(上限と下限)
を計算し二点間の区間内に
母集団のパラメータが含まれる
という表現を用いて推定する
正規分布の平均値の区間推定を考える
確率変数\(x_1,x_2…x_n\)が正規分布に従う時の
以下の性質を利用して母平均の区間推定を考える
標準正規分布
95%内の区間を信頼区間
その境界を臨界点と呼ぶ
2点の臨界点を
確率分布表 Ⅱから求めると

分布で視覚的に確認すると
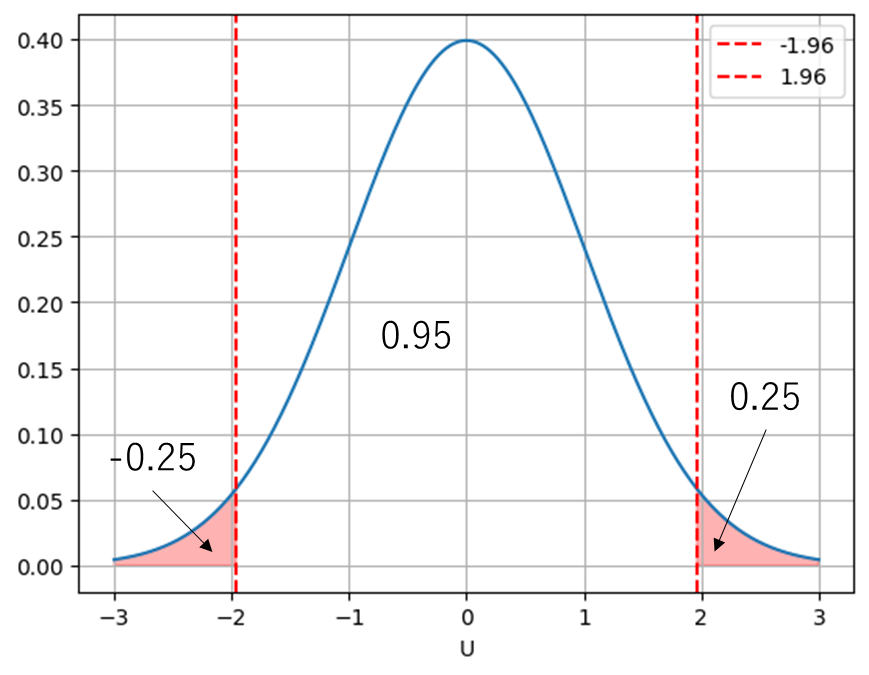
\(P_r(-1.96≦u≦1.96)=0.95\)
\(-1.96≦ \frac{\bar x -μ}{\sqrt {σ_0^2/n}}≦1.96\)を変形すると
\(\bar x -1.96 \sqrt{σ_0^2/n}≦μ≦\bar x +1.96 \sqrt{σ_0^2/n}\)
\(μ\)が区間\((\bar x -1.96 \sqrt{σ_0^2/n},\bar x +1.96 \sqrt{σ_0^2/n})\)
に含まれる確率は95%であることを意味している
区間推定例題
例題1のデータから
母平均の信頼率95%の区間を推定せよ
ただし\(σ_0^2\)は既知で\(σ_0^2=5.0\)とする
| No | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| データ | 10 | 10.5 | 9.5 | 12 | 9 | 7 | 8.5 | 12 | 14 | 12 |
\(Pr(-1.96≦u≦1.96)=0.95\)より
\(\bar x -1.96 \sqrt{σ_0^2/n}≦μ≦\bar x +1.96 \sqrt{σ_0^2/n}\)
に値を代入していく
\(\bar x=10.45,σ_0^2=5.0,n=10\)より
\(10.45 -1.96 \sqrt{5/10}≦μ≦\bar x +1.96 \sqrt{5/10}\)
9.06≦μ≦11.83
母平均の信頼率95%の信頼区間は(9.06,11.83)
参考文献


3章検定と推定の考え方より
まとめ
母平均μの推定手順(σ既知)
点推定:\(\hat μ = \bar x\)
区間推定:信頼率95%の区間μの信頼区間
\((\bar x -1.96 \sqrt{σ_0^2/n} , \bar x +1.96 \sqrt{σ_0^2/n})\)
信頼率99%,90%にしたい時は2.576,1.645とする