今回はカイの二乗検定を
利用して
1つの母集団の分散の
検定と推定を行っていきます。
R]※本サイトにはプロモーションが含まれています
目次
カイの二乗分布
母分散\(σ\)が
ある基準の母分散\(σ_0\)から
変化しているか確認するため
検定を行うには母分散\(σ_0\)から
標本を取得し
検定統計量\(x^2\)を計算し
検定を行う必要がある
\(x_1,x_2,x_3…x_n\)が互いに独立に\(N(μ,σ^2)\)
に従う時\(x^2=\frac{S}{σ^2}\)は自由度\(n-1\)の\(x^2\)分布に従う
母分散\(σ^2\)に関する検定手順
母分散\(σ^2\)に関する検定において
帰無仮説は \(H_0 : σ^2 = σ_0^2\)で
検定統計量は
\(\displaystyle x_0^2 = \frac{S}{σ_0^2}\)
検定手順
1.帰無仮説,条件に適した対立仮説を立てる。
| 仮説 | 式 |
| 帰無仮説 | \(H_0:σ^2=σ_0^2\) |
| 対立仮説 | \(H_1:σ^2\neqσ_0^2\) |
| 対立仮説 | \(H_1:σ^2>σ_0^2\) |
| 対立仮説 | \(H_1:σ^2<σ_0^2\) |
2.有意水準を求める(α=0.05または0.01)
3.帰無仮説\(H_0\)を棄却する棄却域を求める
| 対立仮説 | 棄却域R |
| \(H_1:σ^2\neqσ_0^2\) | \(χ_0^2≦χ^2(Φ,1-α/2)\),\(x_0^2≧χ^2(Φ,α/2)\) |
| \(H_1:σ^2>σ_0^2\) | \(χ_0^2≦χ^2(Φ,1-α)\) |
| \(H_1:σ^2<σ_0^2\) | \(χ_0^2≧χ^2(Φ,α)\) |
4.データ\(x_1,x_2,…x_n\)を取り
検定統計量\(x_0^2\)の値の計算をする
5.\(x_0^2\)の値が棄却域にあれば有意と判定し
\(H_0\)を棄却する
棄却域

有意水準5%の
棄却域を
赤く塗ります
両側検定
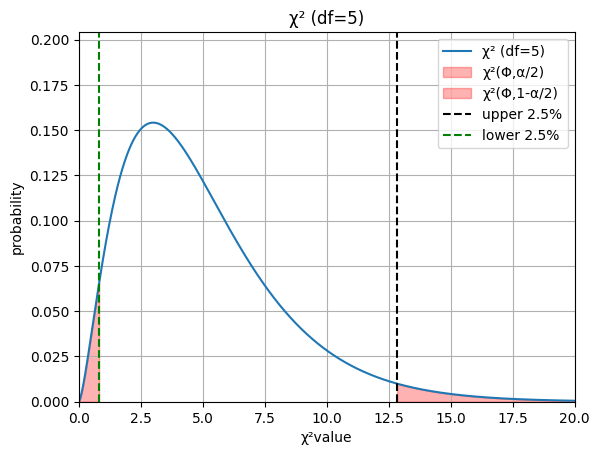
片側検定(上側)
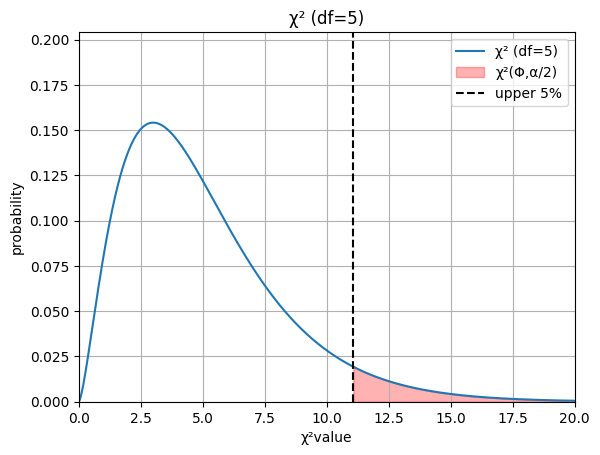
片側検定(下側)
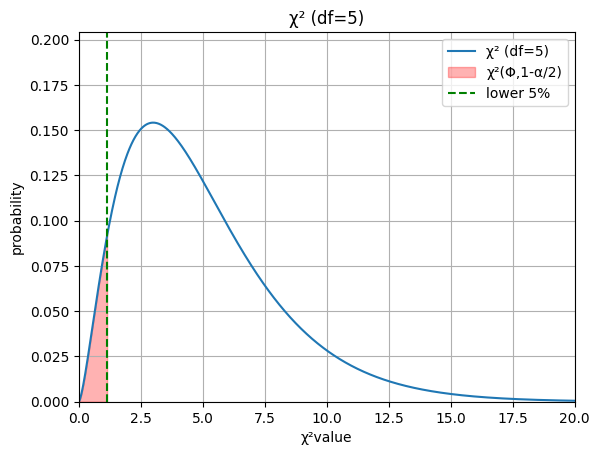

検定統計量が
棄却域に入った時
帰無仮説を
棄却します
\(χ^2\)検定例題
ある工場で精密機械の部品加工を行っていました。
この機械の寸法精度(分散)は\(0.05^2\)である
機械の部品を入れ替えたとき寸法精度が
変化しているか調べよ
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 20.02 | 19.99 | 20.03 | 20.08 | 19.98 | 19.98 | 20.08 | 20.04 | 19.97 | 20.02 |
帰無仮説,対立仮説を設定する
\(H_0:μ=μ_0\)
\(H_1:μ\neq μ_0\)
有意水準αを求める
\(α=0.05\)
棄却域Rを求める
自由度\(Φ=9\)
\(χ_0^2≦χ^2(9,0.975)\),\(x_0^2≧χ^2(9,0.025)\)
確率分布表 より
\(χ^2(9,0.975)=2.7\)
\(χ^2(9,0.025)=19\)
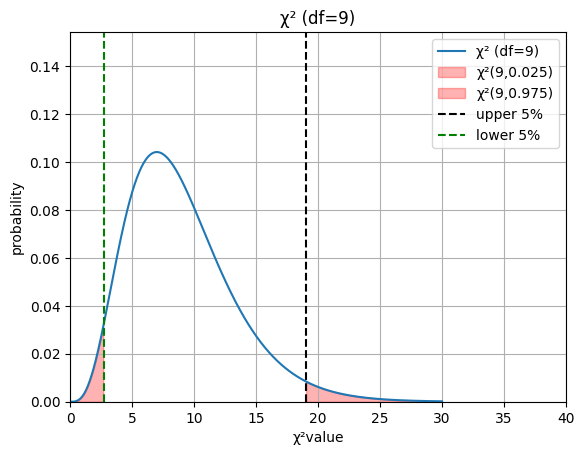
検定統計量を計算
\(\displaystyle S=\sum_{i=1}^{n}x_i^2\)-\(\frac{\displaystyle (\sum_{i=1}^{n}x_i)^2}{n}\)より計算すると
\(S=0.0143\)
検定統計量\(x_0^2\)は
\(\displaystyle x_0^2=\frac{S}{σ_0^2}\)より計算すると
\(\displaystyle x_0^2=\frac{0.0143}{0.05^2}\)
\(x_0^2=5.72\)
検定結果
よって\(x_0^2\)は採択域にあるため有意ではない
部品を入れ替えても寸法精度に変化があるとは言えない
推定
点推定:\(\displaystyle \hat σ^2=\frac{S}{n-1}\)
区間推定:信頼率 \(100(1-α)\)の\(σ^2\)の信頼区間
\(\frac{S}{x^2(Φ,α/2)},\frac{S}{x^2(Φ,1-α/2)}\)
点推定:\(\displaystyle \hat σ^2=\frac{0.0143}{9}\)
\(=0.00158\)
\(\frac{S}{x^2(Φ,α/2)},\frac{S}{x^2(Φ,1-α/2)}\)より
区間推定を計算をすると
\(\displaystyle \frac{0.0143}{19}\)
\(= 0.0007\)
\(\displaystyle \frac{0.0143}{2.7}\)
\(= 0.005\)
[0.0007,0.005]
参考文献


第4章 統計量に関する検定と推定より