[PR]※本サイトには、プロモーションが含まれています
こんにちわ!Yamuです!
前回はカイの二乗検定を
利用して1つの母集団の
分散の検定を行っていきました
今回はF分布の性質を
利用して2つの母集団の
分散を比較,評価する検定について
解説を行っていきます。
・統計検定で問われるF検定について知りたい
1つの母集団の分散の検定
に関してはこちらから!
目次
２つの母分散に関する検定
データA,データBが
それぞれ別の正規分布に従っているとき
検定統計量FはF分布に従います!
イメージだとこんな感じです!
データA,データBをデータ1
データ2に変換して定義を述べると
F分布
\(x_{11},x_{12}….,x_{1n}\)が
互いに独立に\(N(μ_1,σ_1^2)\)に従い
\(x_{21},x_{22}….,x_{2n}\)が
互いに独立に\(N(μ_2,σ_2^2)\)に従う時
\(\displaystyle F=\frac{V_1/σ_1^2}{V_2/σ_2^2}\)は
自由度\(n_1-1,n_2-1\)のF分布に従う
F分布の性質
F分布の特徴を纏めました!
- F分布では自由度が二つある\(Φ_1,Φ_2\)
- F検定を行うにはF分布表を使用する
- \(F(Φ_1,Φ_2:1-P)=\displaystyle \frac{1}{F(Φ_2,Φ_1:P)}\)
の関係が成り立つ - \(P=Pr(F≧F(Φ_1,Φ_2:P))\)の分布を確認すると
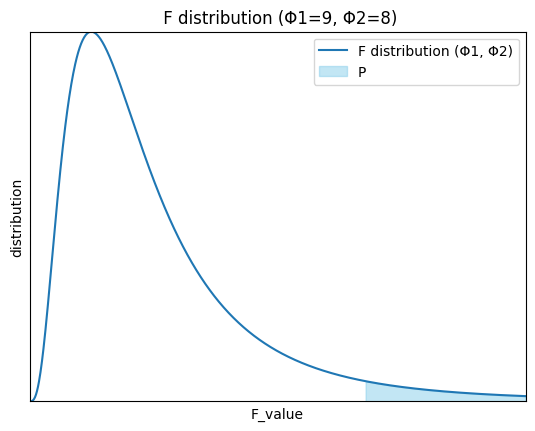
２つの母分散に関するF検定手順
最初にF検定の手順を紹介します。
検定の基本的な考え方は
こちらの記事で確認できます！
1.帰無仮説対立仮説を立てる
| 仮説 | 記号 |
| 帰無仮説 | \(H_0:σ_1^2=σ_2^2\) |
| 対立仮説(両側検定) | \(H_1:σ_1^2\neqσ_2^2\) |
| 対立仮説(片側検定) | \(H_1:σ_1^2>σ_2^2\) |
| 対立仮説(片側検定) | \(H_1:σ_1^2<σ_2^2\) |
2.有意水準を求める(α=0.05または0.01)
3.帰無仮説\(H_0\)を棄却する棄却域を求める
| 仮説 | 棄却域 |
| \(H_1:σ_1^2\neqσ_2^2\),\(V_1>V_2\) | \(\displaystyle F_0=\frac{V_1}{V_2}≧F(Φ_1,Φ_2,α/2)\) |
| \(H_1:σ_1^2\neqσ_2^2\),\(V_1<V_2\) | \(\displaystyle F_0=\frac{V_2}{V_1}≧F(Φ_2,Φ_1,α/2)\) |
| \(H_1:σ_1^2>σ_2^2\) | \(\displaystyle F_0=\frac{V_1}{V_2}≧F(Φ_1,Φ_2,α)\) |
| \(H_1:σ_1^2<σ_2^2\) | \(\displaystyle F_0=\frac{V_2}{V_1}≧F(Φ_2,Φ_1,α)\) |
4.2つの母集団から検定統計量\(F_0\)を計算する
\(V_1>V_2\)
\(F_0=\frac{V_1}{V_2}\)
\(V_1<V_2\)
\(F_0=\frac{V_2}{V_1}\)
5.\(F_0\)の値が棄却域に入っていれば有意とし
\(H_0\)を棄却する
実際に例題を利用して
F検定を行っていきます
F検定
ある工場で機械1と機械2を利用して
飲料をビンに詰める工程があった
目標は100gである
機械1で作った製品と機械2で作った製品を10個
ずつ取得した結果以下のデータが得られた
| No | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 機械1 | 99.8 | 99.5 | 99.4 | 98.8 | 100.2 | 100.7 | 100.5 | 99.6 | 99.2 | 99 |
| 機械2 | 99.8 | 101 | 99.6 | 98 | 100.3 | 100.7 | 100.4 | 99.8 | 99.6 | 99.8 |
機械1の分散\(σ_1\)と機械2の分散\(σ_2\)が一致しているか検定せよ
帰無仮説,対立仮説を立てる
帰無仮説:\(H_0:σ_1^2=σ_2^2\)
対立仮説:\(H_1:σ_1^2\neqσ_2^2\)
有意水準を求める
\(α=0.05\)
棄却域を求める
\(V_1>V_2\)の場合
\(\displaystyle F_0=\frac{V_1}{V_2}≧F(Φ_1,Φ_2,α/2)\)
\(V_1<V_2\)の場合
\(\displaystyle F_0=\frac{V_2}{V_1}≧F(Φ_2,Φ_1,α/2)\)
\(V_1とV_2\)の大小関係に
よって棄却域を使い分けます!
検定統計量の計算
\(H_0:σ_1^2=σ_2^2\)より
\(σ_1^2=σ_2^2\)と仮定しているので
統計量\(F_0\)は
\(F_0=\frac{V_1}{V_2}\)
もしくは
\(F_0=\frac{V_２}{V_1}\)
機械1から\(V_1\),機械2から\(V_2\)
を求める
\(V_1=\frac{S_1}{n-1}\)より
\(V_1=\frac{3.581}{9}=0.397\)
\(V_2=\frac{S_2}{n-1}\)
\(V_2=\frac{6.08}{9}=0.676\)
\(V_2＞V_1\)より
\(F_0=\frac{V_２}{V_1}\)
\(F_0=\frac{0.676}{0.397}\)
\(F_0=1.7\)
有意かどうか判定をする
\(F(9,9,0.025)\)はF分布表より
\(F(9,9,0.025)=4.03\)
\(\displaystyle F_0=\frac{V_2}{V_1}≦F(Φ_2,Φ_1,α/2)\)
より有意ではない
\(H_1:σ_1^2\neqσ_2^2\)とは言えない
推定
点推定と区間推定について紹介していきます。
2つの母分散の比の推定
\(\hat{σ_1^2/σ_2^2}=V_1/V_2\)
信頼率95%区間
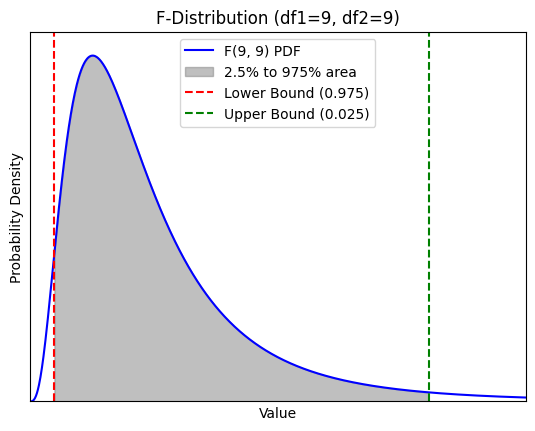
\(\displaystyle F(Φ_1,Φ_2,1ーα/2)≦\frac{V_1/σ_1^2}{V_2/σ_2^2}≦F(Φ_1,Φ_2,α/2)\)
\(\displaystyle \frac{V_1}{V_2}・\frac{1}{F(Φ_1,Φ_2,α/2)}≦\frac{σ_1^2}{σ_2^2}≦ \frac{V_1}{V_2}・\frac{1}{F(Φ_1,Φ_2,/1-2α)}\)
\(\displaystyle \frac{V_1}{V_2}・\frac{1}{F(Φ_1,Φ_2,α/2)}≦\frac{σ_1^2}{σ_2^2}≦ \frac{V_1}{V_2}・F(Φ_1,Φ_2,α/2)\)
\(\displaystyle \hat{σ_1^2/σ_2^2}=(\frac{V_1}{V_2}・\frac{1}{F(Φ_1,Φ_2,α/2)},\frac{V_1}{V_2}・F(Φ_1,Φ_2,α/2))\)
例題の母分散の比の点推定と区間推定
\(\hat{σ_1^2/σ_2^2}=0.397/0.676\)
\(=0.587\)
95%の信頼区間は
\(\displaystyle \hat{σ_1^2/σ_2^2}=(\frac{0.397}{0.676}・\frac{1}{F(9,9,0.025)},\frac{0.397}{0.676}・F(9,9,0.025))\)
\(0.145,2.36\)
推定まとめ
点推定:\(\hat{σ_1^2/σ_2^2}=V_1/V_2\)
区間推定:\(\displaystyle (\frac{V_1}{V_2}・\frac{1}{F(Φ_1,Φ_2,α/2)},\frac{V_1}{V_2}・F(Φ_1,Φ_2,α/2))\)
参考文献
まとめ
F分布の性質を利用して2つの母集団の
分散を比較,評価する検定について解説を行っていきました。
