離散確率分布
連続確率分布について
例題やpythonを使って
説明していきます
[PR]※本サイトにはプロモーションが含まれています
確率とは?
確率とはある事柄(事象)Aが起こる
確からしさを数値で表したものである
記号で表すと\(P(A)\)
事象Aが起こる確率は
以下のような決まりがあります!
\(0≦P(A)≦1\)
確率分布とは?
確率分布(Probability Distribution)は
ある事象が発生する確率を示す
数学的なモデル、関数のことを指します
データは計量値と計数値に分類できる
それに対応して確率分布は
連続モデル(連続確率分布)と
離散モデル(離散確率分布)
があります
確率変数とは?
確率変数(Probability Variable)は
実験や観測,試行によって
出た値の事を示します
この値は確率的に変動するので
確率変数と言います
例えばサイコロを振る実験を行った時
サイコロの出る目は{1,2,3,4,5,6}で
1~6まで取りえる値の確率が与えられるので
この値は確率変数になる。
確率変数はXを用いて表される
\(X=(x_1,x_2,x_3…x_n)\)

サイコロの目は
確率変数なんだね!
離散確率分布(Discrete Distribution)
離散分布(Discrete Distribution)とは
特定の離散的な値(個別の値)
をとる確率変数の分布のことを指します。
例えばサイコロを1回投げる時に出る目をXとすれば
1 ~ 6の離散的な値をとります
これを離散型確率変数と呼びます
この離散型確率変数は
確率分布を持っています
離散確率分布を表す関数は
\(f_i=P_r(x=x_i)\)

\(x_i\)になる確率は\(f_i\)
ってことかな~
\(f_i\)は次の性質を持つ
\(f_i≧0\)
\(\displaystyle \sum_{K=1}^{∞}f_i=1\)

式だけじゃ
わからないよ~
サイコロの離散分布
サイコロの出る目は1から6である。
以下の表に出る目の確率を表記する
| 確率変数 | 確率関数 | 確率の記号 | 一様分布 |
| 1 | \(f_1\) | \(P_r(x_1)\) | \(\displaystyle \frac{1}{6}\) |
| 2 | \(f_2\) | \(P_r(x_2)\) | \(\displaystyle \frac{1}{6}\) |
| 3 | \(f_3\) | \(P_r(x_3)\) | \(\displaystyle \frac{1}{6}\) |
| 4 | \(f_4\) | \(P_r(x_4)\) | \(\displaystyle \frac{1}{6}\) |
| 5 | \(f_5\) | \(P_r(x_5)\) | \(\displaystyle \frac{1}{6}\) |
| 6 | \(f_6\) | \(P_r(x_6)\) | \(\displaystyle \frac{1}{6}\) |

確率変数が1になる
確率関数は\(\frac{1}{6}\)
ってことかな!?
縦軸に確率の値、横軸に確率変数を取ると
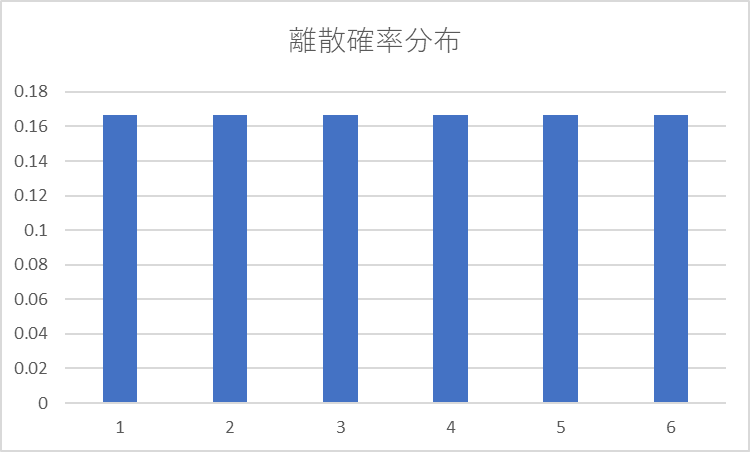

\(\displaystyle \frac{1}{6}\)で離散的に
確率が分布してますね!
累積分布を確認すると\(\displaystyle \sum_{1}^{6}f_i=1\)が確認できる


サイコロの出目は
1~6までしか
出ないから
全部の確率足したら
1になるんだね~
連続確率分布
測定値から作られるデータを
連続確率変数と呼ぶ
連続確率変数から
作られる確率分布が
連続確率分布である
連続確率分布の代表的なモデルは
正規分布である。
正規分布はヒストグラムから拡張できる
この記事を参照してください
平均値0ばらつき1の元の
連続変数から作られる確率分布は以下の図になります
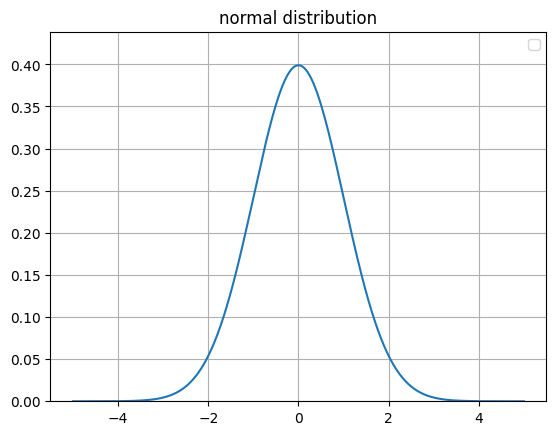
全ての確率変数はこの分布内に収まるので
x軸と正規分布で囲まれている面積 = 1
となる
\(\displaystyle P_r(a≦x≦b)=\int_a^bf(x)dx=1\)
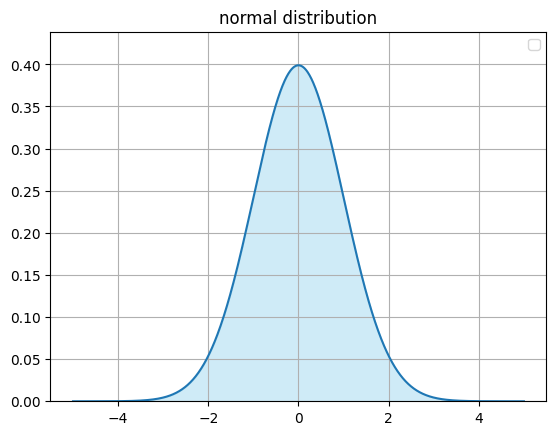
次に-2から0に囲まれている部分を考える
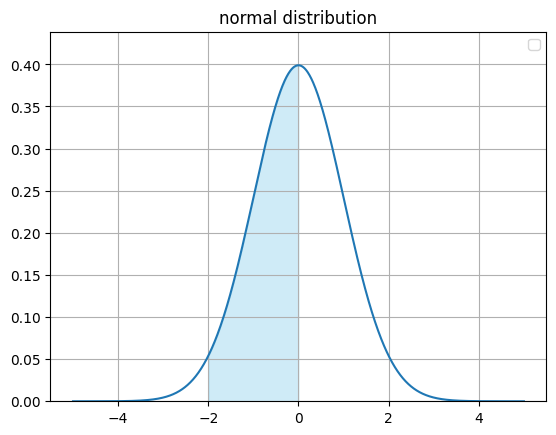
この面積は確率変数が
-2 ≦ x ≦ 0
を満たす確率だと考えられる
\(\displaystyle P_r(a ≦ x ≦ b) = \int_a^bf(x)dx\)

連続確率分布は
面積が確率に
なるんだね!
おまけ正規分布のレシピ
正規分布のレシピ
import numpy as np
import matplotlib.pyplot as plt
# データの範囲を設定
x = np.linspace(-5, 5, 1000)
# 標準正規分布の確率密度関数
pdf = (1/np.sqrt(2*np.pi)) * np.exp(-x**2 / 2)
# グラフの描画
plt.plot(x, pdf)
plt.fill_between(x, pdf, where=(x >= -2) & (x <= 0), color='skyblue', alpha = 0.4)
plt.title('normal distribution')
plt.ylim(0, max(pdf)*1.1) # y軸の範囲を設定、0から最大値の少し上まで
plt.legend()
plt.grid(True)
plt.show()