今回は
ヒストグラムから
確率密度関数を
pythonを使って
作っていきます
[PR]※本サイトには、プロモーションが含まれています
目次
ヒストグラム(histogram)とは?
連続データの分布を
視覚的に表現するためのグラフ
縦軸を度数、横軸を各区間に分け
グラフを作ります
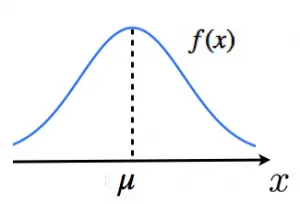
確率密度関数とは
連続的な値をとる確率変数の発生のしやすさを
関数で表したもの
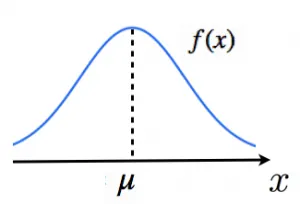
以下の式が成り立ちます
\(\int_{-\infty}^{\infty}f(x)dx = 1\)
この式はf(x)の曲線と軸で
囲まれた面積が1で
あることを示します
確率変数xがある区間から
ある区間を満たす確率は
以下の公式で考えることが出来る
\(Pr(a≦x≦b) = \int_{a}^{b}f(x)dx\)
\(Pr(a≦x≦b)\) = (a≦x≦bとなる部分の面積)
ヒストグラムから確率密度関数へ
まずはデータを用意します
次に度数表を用意してデータを分けます
| 階級範囲 | 階級 | 度数 |
| 1 ~ 10 | 1 | 2 |
| 11 ~ 20 | 2 | 2 |
| 21 ~ 30 | 3 | 4 |
| 31 ~ 40 | 4 | 3 |
| 41 ~ 50 | 5 | 2 |
| – | 合計 | 13 |
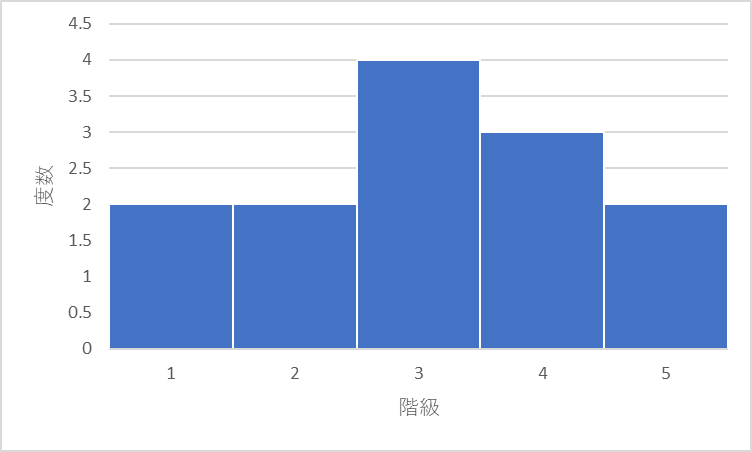
データのサイズは13なので13で度数を割ります
| 階級範囲 | 階級 | 度数 | 相対度数 |
| 1 ~ 10 | 1 | 2 | 0.154 |
| 11 ~ 20 | 2 | 2 | 0.154 |
| 21 ~ 30 | 3 | 4 | 0.308 |
| 31 ~ 40 | 4 | 3 | 0.231 |
| 41 ~ 50 | 5 | 2 | 0.154 |
| – | 合計 | 13 | 1.0 |
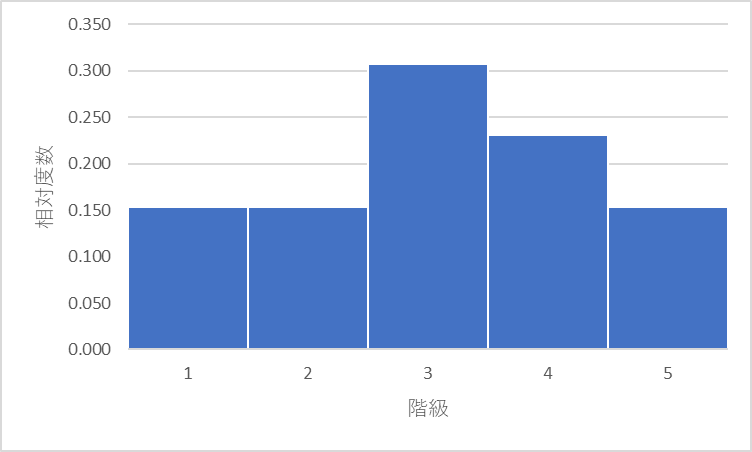
データを取った時に
1 ~ 10の間に入る確率が15.4%
11~20の間に入る確率が15.4%
21~30の間に入る確率が30.8%
31~40の間に入る確率が23.1%
41~50の間に入る確率が15.4%
といったことを示すグラフになります
今はデータの数 n =13 , 区間幅9ですが
データ数を無限(∞),区間幅を0にすると
ヒストグラムの輪郭は
滑らかな曲線にになります
この滑らかな曲線を
確率密度関数といいます
Pythonでヒストグラムから確率密度関数へ
n→∞ , C→0の操作を疑似的に
pythonで行って
ヒストグラムの輪郭が滑らかになるか確かめる
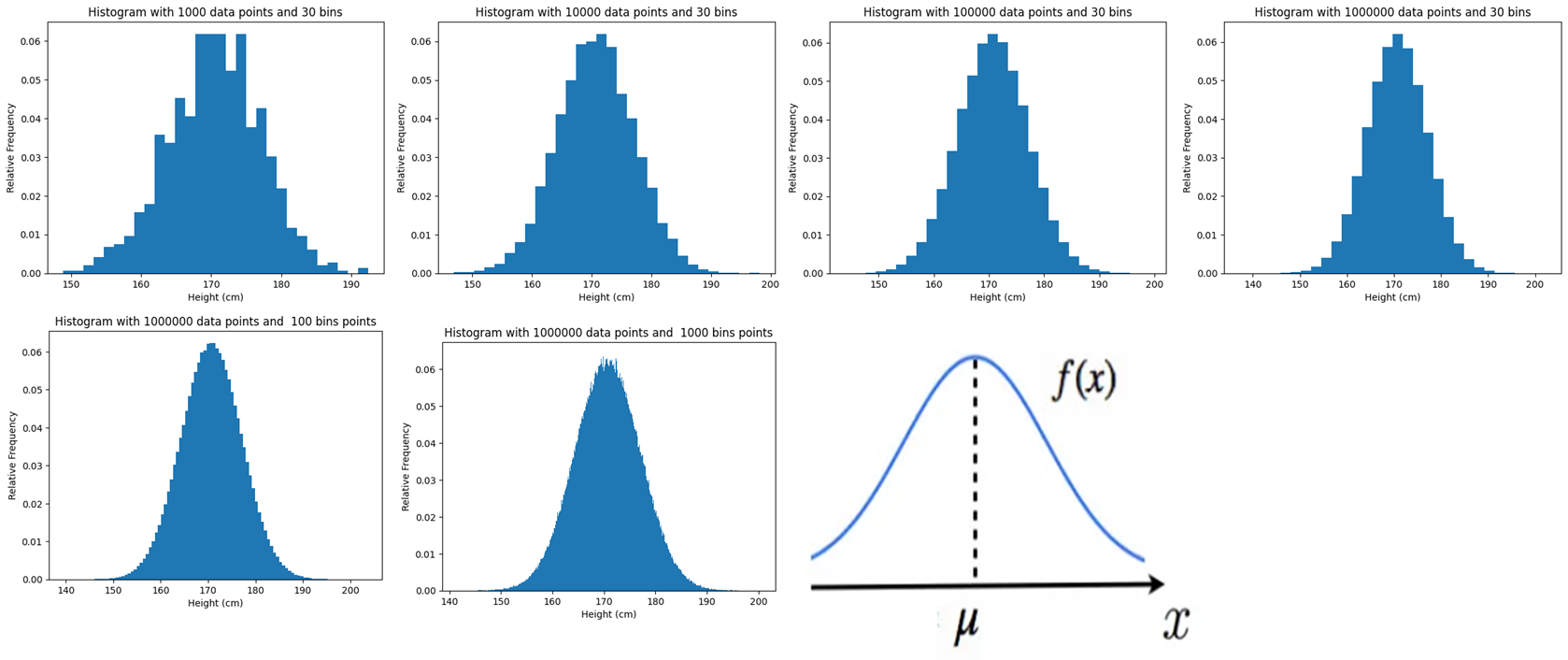
データの数nを増やす
区間の数は100固定で
データサイズを
1000→10000→100000→1000000
と変化させてヒストグラムを観察する
| データ名 | データの種類 | データサイズ | 区間の数 |
| データ 1 | 日本人成人男性の身長データ | 1000 | 30 |
| データ 2 | 日本人成人男性の身長データ | 10000 | 30 |
| データ 3 | 日本人成人男性の身長データ | 100000 | 30 |
| データ4 | 日本人成人男性の身長データ | 1000000 | 30 |
下記のコードを使って
データサイズをシフトさせながら
ヒストグラムを実装していきます
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
counta = [1000, 10000,100000,1000000]
for n in counta:
japan_man = np.random.normal(170.7, 6.4, n)
plt.hist(japan_man, bins=30, density=True)
plt.title(f'Histogram with {n} data points and 30 bins')
plt.xlabel('Height (cm)')
plt.ylabel('Relative Frequency')
plt.show()
出力結果


なんか輪郭が
滑らかになってきてる
ように見える!
Bin数を増やす
データサイズを1000000に固定し
bin数をshiftさせていく
| データ名 | データの種類 | データサイズ | 区間の数 |
| データ 5 | 日本人成人男性の身長データ | 1000000 | 100 |
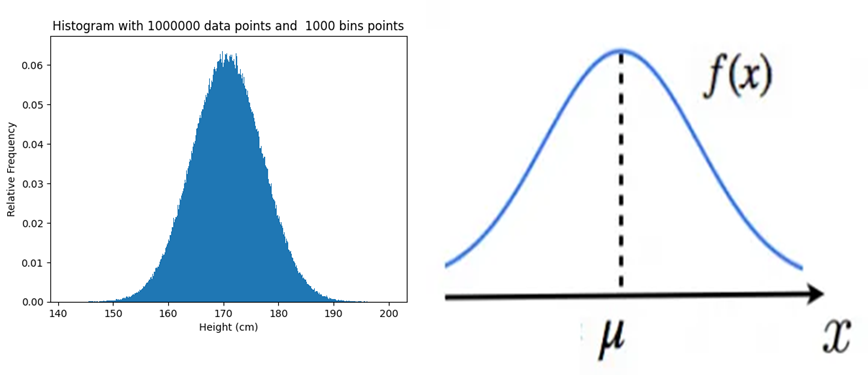
| データ 6 | 日本人成人男性の身長データ | 1000000 | 1000 |
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
counta = [100, 1000]
for n in counta:
japan_man = np.random.normal(170.7, 6.4, 1000000)
plt.hist(japan_man, bins=n, density=True)
plt.title(f'Histogram with 1000000 data points and {n} bins points')
plt.xlabel('Height (cm)')
plt.ylabel('Relative Frequency')
plt.show()出力結果
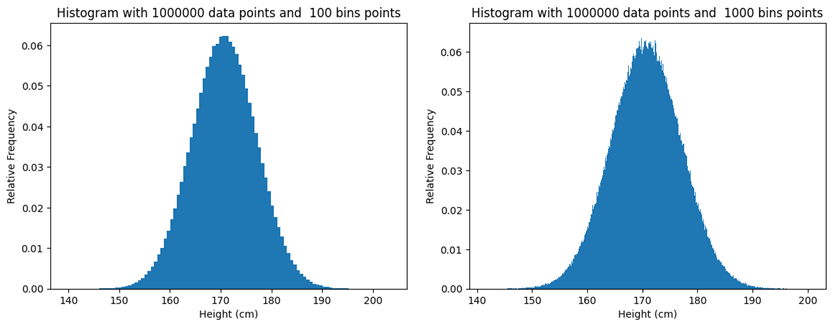

輪郭が丸くなってる!
まとめ
正規化したヒストグラムに
n→∞ , c→0の操作を行うと
ヒストグラムは確率密度関数になる