Pythonを使ってQ-Qプロットを作ろう

こんにちわ!Yamuです。
昔の記事でq-qプロットに
関して説明していきました。
今回はpythonを利用して
様々なq-q プロットを作成
していきます

この記事はこんな人におススメ

・pythonを利用してq-qプロットを作成したい

合わせて読みたい

1 Q-Q plot
2 参考文献
3 まとめ

Q-Q plot

正規分布に基づく2つのデータ群をQ-Qプロットにする

今回使うデータを表にしました。

データサイズ	データラベル	データに対応する確率分布
1000	Data1	\(N(0,1)\)
1000	Data2	\(N(1,1)\)

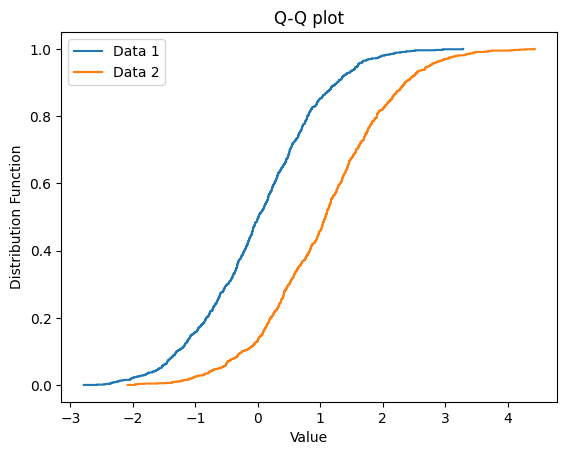
分布が綺麗に
二つに分かれていますね!

import numpy as np
import matplotlib.pyplot as plt

def empirical_distribution_function(data):
    # データを昇順にソート
    sorted_data = np.sort(data)
    
    # データ点ごとの累積相対頻度を計算
    n = len(sorted_data)
    y = np.arange(1, n + 1) / n
    
    return sorted_data, y

# 例として、二つのデータセットを生成
data1 = np.random.normal(loc=0, scale=1, size=1000)
data2 = np.random.normal(loc=1, scale=1, size=1000)

# 経験分布関数を計算
x1, y1 = empirical_distribution_function(data1)
x2, y2 = empirical_distribution_function(data2)

# プロット
plt.step(x1, y1, label='Data 1', where='post')
plt.step(x2, y2, label='Data 2', where='post')

# ラベルやタイトルの設定
plt.xlabel('Value')
plt.ylabel('Distribution Function')
plt.title('Q-Q plot')

# 凡例の表示
plt.legend()

# グラフの表示
plt.show()

正規分布に基づく2つのデータ群を1つのQ-Qプロットにする

2つのデータ群を1つに纏めて
q-qプロットを引いてみます。

データサイズ	データラベル	データに対応する確率分布
2000	Combined Data	\(N(0, 1) or N(5, 1)\)

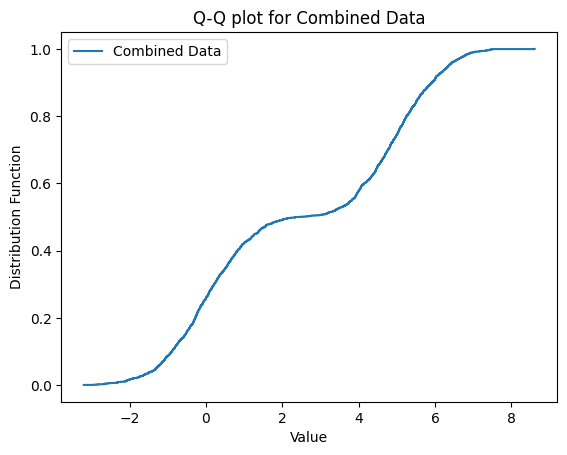
2つの分布が積層したものはこのような
形になるんですね!

import numpy as np
import matplotlib.pyplot as plt

def empirical_distribution_function(data):
    sorted_data = np.sort(data)
    n = len(sorted_data)
    y = np.arange(1, n + 1) / n
    return sorted_data, y

# 例として、二つのデータセットを生成
data1 = np.random.normal(loc=0, scale=1, size=1000)
data2 = np.random.normal(loc=5, scale=1, size=1000)

# データを結合
combined_data = np.concatenate([data1, data2])

# 経験分布関数を計算
x_combined, y_combined = empirical_distribution_function(combined_data)

# プロット
plt.step(x_combined, y_combined, label='Combined Data', where='post')

# ラベルやタイトルの設定
plt.xlabel('Value')
plt.ylabel('Distribution Function')
plt.title('Q-Q plot for Combined Data')

# 凡例の表示
plt.legend()

# グラフの表示

複数のデータ群をQ-Q plotにする

最後に複数のデータ群を
ループ構文を利用して
q-q plotにしていきます

データサイズ	データラベル	データに対応する確率分布
1000	Data1	\(N(0,1)\)
1000	Data2	\(N(1,1)\)
1000	Data3	\(N(2,1)\)
1000	Data4	\(N(3,1)\)
1000	Data5	\(N(4,1)\)

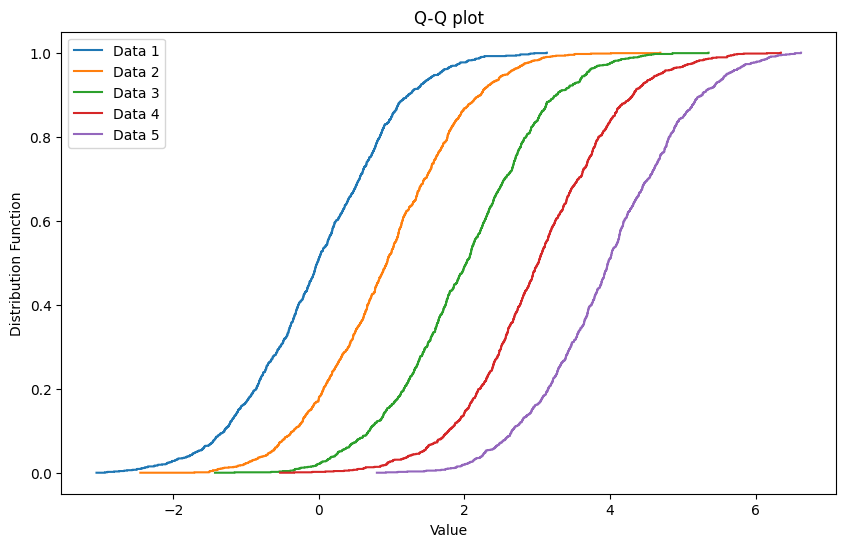
5つの分布が綺麗に
わかれましたね!

import numpy as np
import matplotlib.pyplot as plt

def empirical_distribution_function(data):
    sorted_data = np.sort(data)
    n = len(sorted_data)
    y = np.arange(1, n + 1) / n
    return sorted_data, y

# データセットの数
num_datasets = 5

# プロットの準備
plt.figure(figsize=(10, 6))

# データセットを生成してプロット
for i in range(num_datasets):
    data = np.random.normal(loc=i, scale=1, size=1000)
    x, y = empirical_distribution_function(data)
    plt.step(x, y, label=f'Data {i+1}', where='post')

# ラベルやタイトルの設定
plt.xlabel('Value')
plt.ylabel('Distribution Function')
plt.title('Q-Q plot')

# 凡例の表示
plt.legend()

# グラフの表示
plt.show()

Q-Q plotにlimit線を入れる

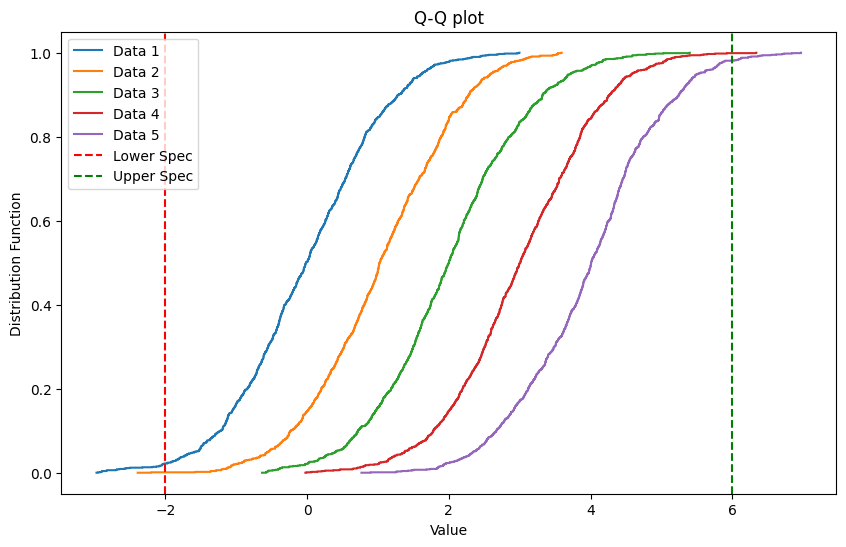
limit線を入れることで
limit線内に分布が
入っているか
確認できます!

import numpy as np
import matplotlib.pyplot as plt

def empirical_distribution_function(data):
    sorted_data = np.sort(data)
    n = len(sorted_data)
    y = np.arange(1, n + 1) / n
    return sorted_data, y

# データセットの数
num_datasets = 5

# プロットの準備
plt.figure(figsize=(10, 6))

# データセットを生成してプロット
for i in range(num_datasets):
    data = np.random.normal(loc=i, scale=1, size=1000)
    x, y = empirical_distribution_function(data)
    plt.step(x, y, label=f'Data {i+1}', where='post')

# 上限スペックと下限スペックを設定
lower_spec = -2
upper_spec = 6

# 上限スペックと下限スペックをプロット
plt.axvline(lower_spec, color='r', linestyle='--', label='Lower Spec')
plt.axvline(upper_spec, color='g', linestyle='--', label='Upper Spec')

# ラベルやタイトルの設定
plt.xlabel('Value')
plt.ylabel('Distribution Function')
plt.title('Q-Q plot')

# 凡例の表示
plt.legend()

# グラフの表示
plt.show()

参考文献

まとめ

今回はpythonを利用して
様々なq-q プロットを作成
していきました。
ありがとうございました!