今回は
ヒストグラムの種類
相対頻度ヒストグラム
累積分布について
説明していきます
[PR]※本サイトにはプロモーションが含まれています
目次
ヒストグラムの役割

ヒストグラムの
役割は測定値などの
連続的なデータが
どのような分布を
持っているか
確認することです
数値の分布を
グラフ化することに
よって視覚から
データの傾向を
掴むことができます
ヒストグラムの種類

ヒストグラムを
紹介していきます
一般形(山型)
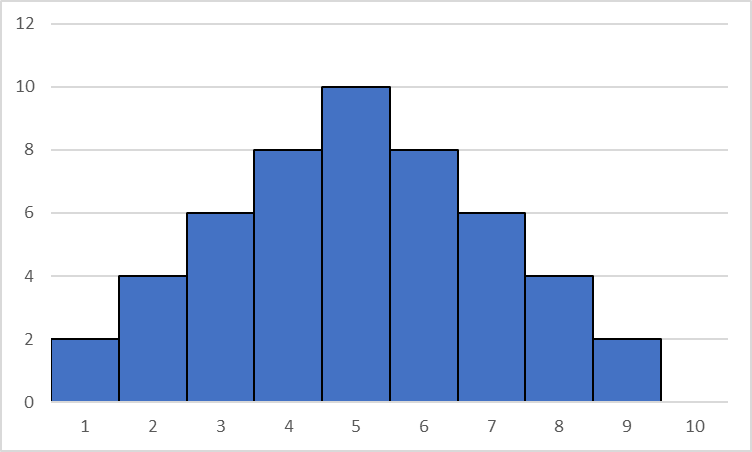
中心が高くなり分布が左右対称に近い形状になる。
「正規分布」に近い一般的な形である。
自然な確率分布なので
品質管理ではこの状態は
工程が安定的状態にあるといわれている。
ふた山型
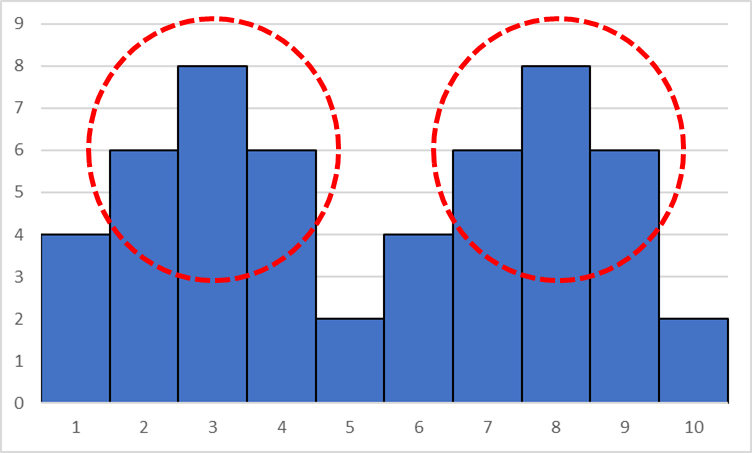
分布が高くなっている所が二つ存在し
「二つの山」のようになっている形状である。
異なる分布を持った「二つの集団が積層」している可能性がある。
例:青森産のリンゴの重さの分布と
北海道産のリンゴの重さを一緒に図った時の分布など
歯抜け型
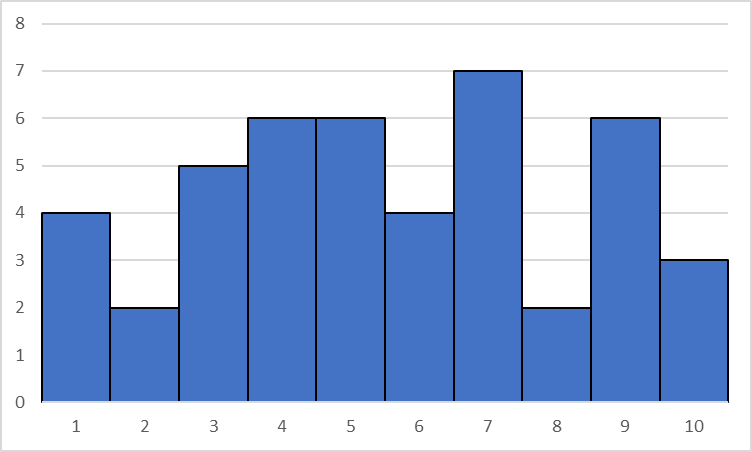
区間の形状に規則性がなく全体的に見たとき
歯が抜けたような形状、データ数(サンプル数)が不十分、
適切な区間数(bin)でない。
サンプリング方法、サンプリング数やBin数を見直す必要がある。
左裾型
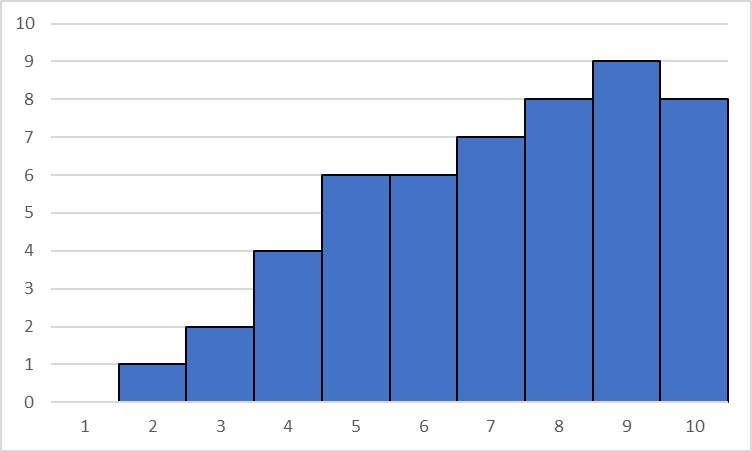
グラフ右に分布が偏っている形状、
分布に上限値があり上限
を取り除いた時現れる分布である。
- 工場で製品の全数検査を行った時、上限値を超えたものを全て取り除いた製品の分布など
- 100点満点のテストの点数分布など
右裾型
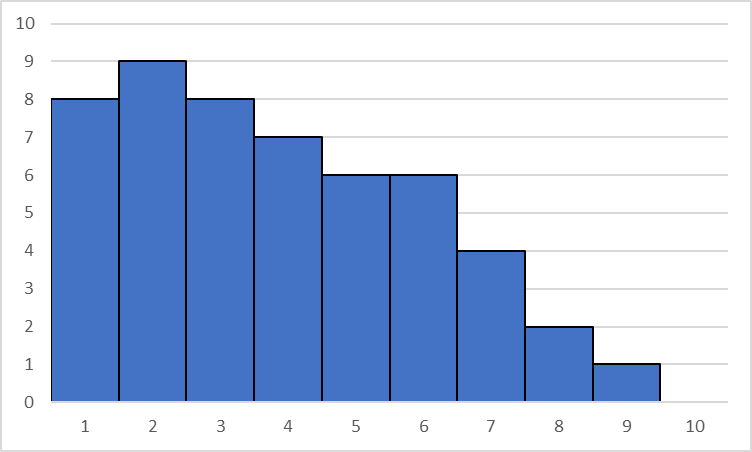
グラフ左に分布が偏っている形状、
分布に下限値があり下限を
取り除いた時現れる分布である。
離れ小島型
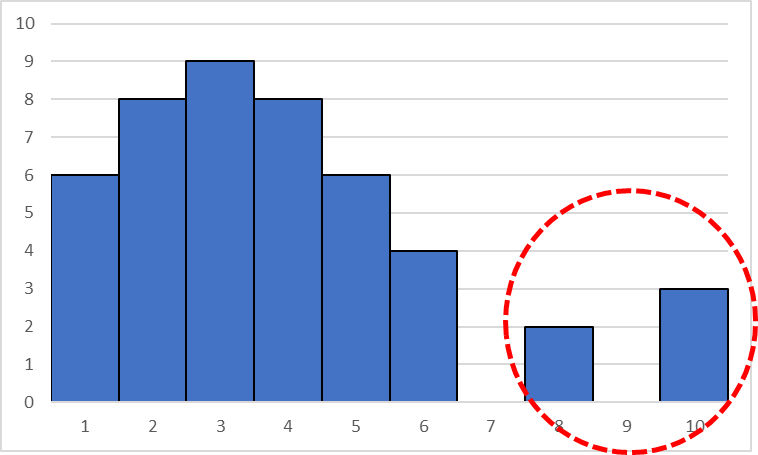
分布の外に離れている値があるのが特徴、
離れている値は突発的な不良、事故等で
発生したものだと推測できます。
相対頻度ヒストグラム(Frequency Histogram)
各階級の頻度をデータ全体のサイズで割った
縦軸が相対頻度を示すヒストグラムです。
相対頻度は、各階級の割合(確率)を表します

サンプルサイズ(51)で度数を割り
データが各階級に入る確率を求めます。

ヒストグラムにすると
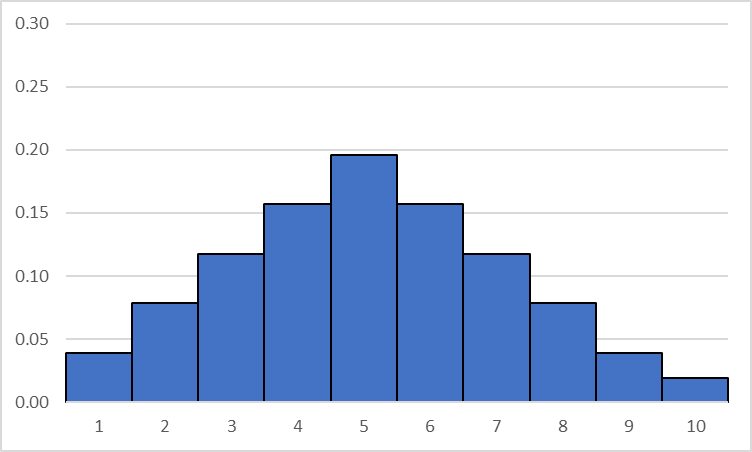
相対度数が一番大きいものは区間5で0.2です。
これだと分かりにくいのでパーセンテージ[%]に直すと
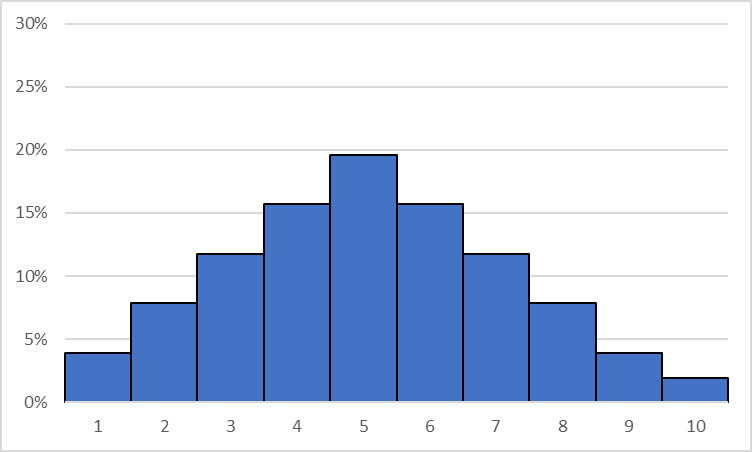

各区間に
収まる確率に
なりましたね!
累積ヒストグラム(Cumulative Histogram)
累積ヒストグラムは、
一番下の階級から
相対度数から
累積度数を作ります

累積度数をグラフにすると
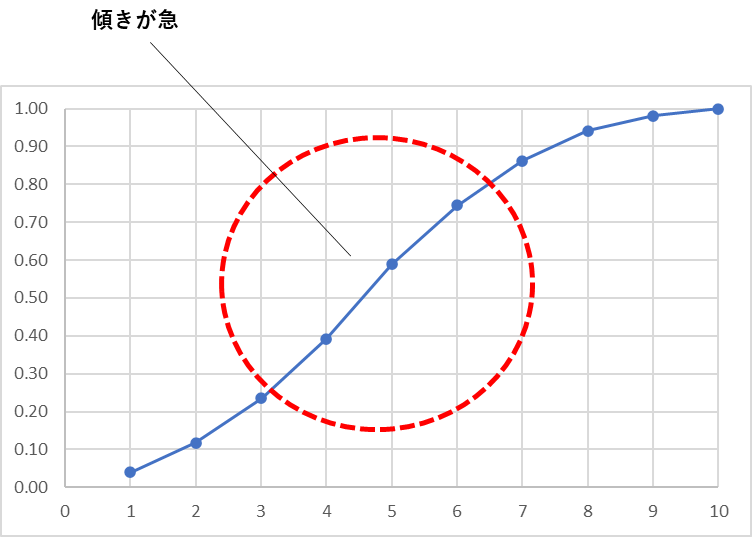
傾きが急になっているので
データは区間4,5,6の分布に
集中していることが分かります。