製品品質の評価のための仮説検定の考え方

R]※本サイトにはプロモーションが含まれています

製品の品質問題

部品Aを製造している工場がある。

工場のある工程(装置)で

部品Aを作っている

部品Aの寸法は10umとなるように設定している

しかし装置Aで作った製品は

設定値10umからずれているのではないか?

と現場で疑われている。

そこでデータをサンプリングして確かめることにする。

1	2	3	4	5	6	7	8	9	10
10.5	10.8	9.7	8.8	10.5	10.8	11	10.2	10.5	10.2

平均値\(\bar x\)を求めてみます

\(\frac{10.5+10.8+9.7+8.8+10.5+10.8+11+10.2+10.5+10.2}{10}\)

\(\bar x=10.3\)

結果\(\bar x=10.3\)によって

装置Aから作られている部品Aは

設定値よりずれているかどうか判断できるでしょうか?

このずれているかどうかを統計的に

客観的に判断する手法として

‘仮説検定‘

という統計的な手法があります

製品の品質問題に対する仮説検定の立て方

装置Aで作った製品は

設定値10umからずれているのではないか?

ということを実証するために

いくつか仮説を立てます

母集団は部品Aの寸法

部品Aの寸法は正規分布に従う

仮定の話だが

母分散が\(σ^2=0.2\)

部品Aの寸法が正規分布N(μ,0.2)に従うと考える

そして二つの仮説を立てる

このことを次のように表現する

仮説検定では\(H_0\)が成り立っている

条件下の元でデータが不自然であるか

自然であるか議論します

検定統計量の計算

\(H_0\)が成り立っているか確認するために

得られたデータから統計検定量　\(u_0\)を

計算します

得られたデータの平均値は

\(\bar x=10.3\)

\(\displaystyle u_0= \frac{\bar x-μ}{\sqrt{σ^2/n}}\)を計算すると

\(\displaystyle u_0= \frac{10.3-10}{\sqrt{0.2/10}}=2.1\)

統計量\(u_0\)は

N(0,1)の標準正規分布に従う性質を持っている

有意水準を設定する

計算された検定統計量が

\(H_0\)の元で不自然かどうかの

判断として有意水準と棄却域を設定する

例えば有意水準5%にすると

\(u=1.96\)

1.96を基準として

\(❘u_0❘≧1.96\)

の場合有意水準5%を超えるので

棄却域に入るので

\(H_0\)を排除して

\(H_1\)と判定する

\(❘u_0❘<1.96\)

の方は採択域と呼び

この中に\(u_0\)が

入る場合\(H_0\)を採択し

\(H_0\)と判断する

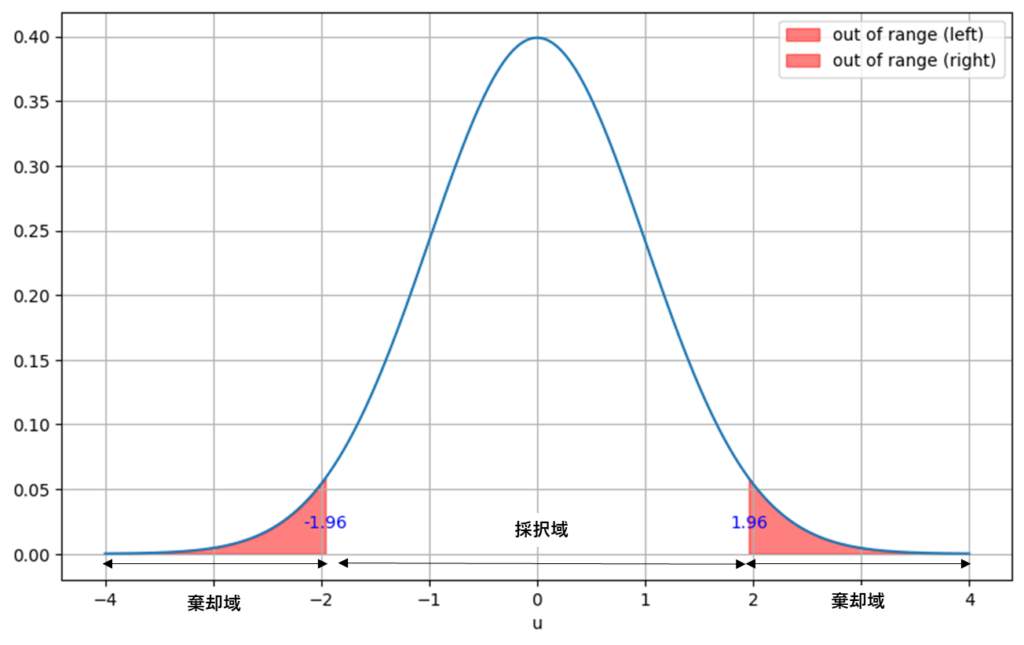
u0の値と有意水準の値を比較して検定を行う

u=2.1より信頼率95%の外にあることが分かりました。

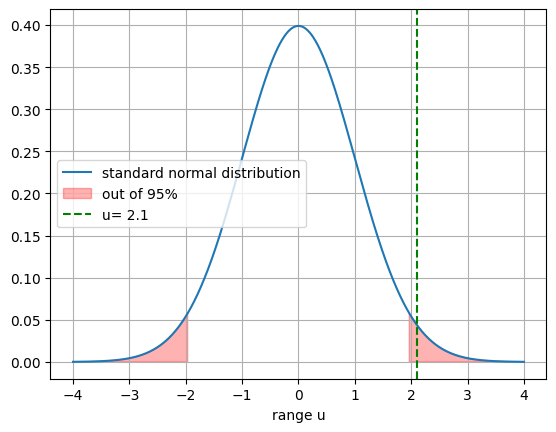
\(u=2.1\)になる確率は\(H_0\)

の元では5%以下です

もしこの装置Aが\(μ=10\)で

作れる能力を持っているのであれば

取得したデータの平均値になる確率が

5%以下なので不自然と

考えます。

このような判断を下す一連の流れ

つまり手法を検定と言います。

検定の種類

検定	対立仮説	棄却域
両側検定	\(μ\neqμ_0\)	\(1.96≦❘u_0❘\)
左片側検定	\(μ<μ_0\)	\(-1.645≧u_0\)
右片側検定	\(μ>μ_0\)	\(1.645≦u_0\)

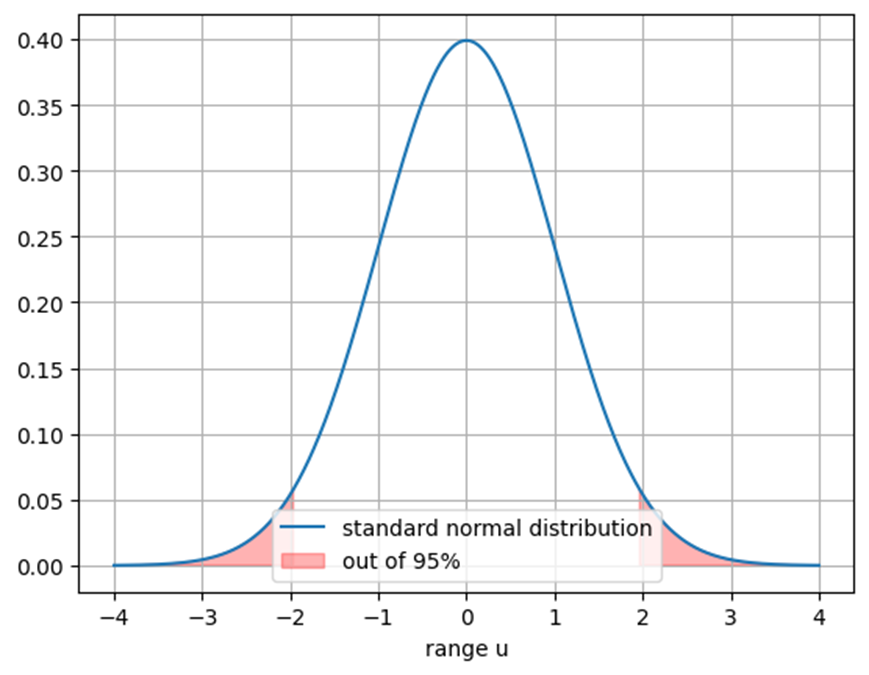
両側検定(5%)

\(1.96≦❘u_0❘\)の時有意

帰無仮説\(H_0\)は棄却される

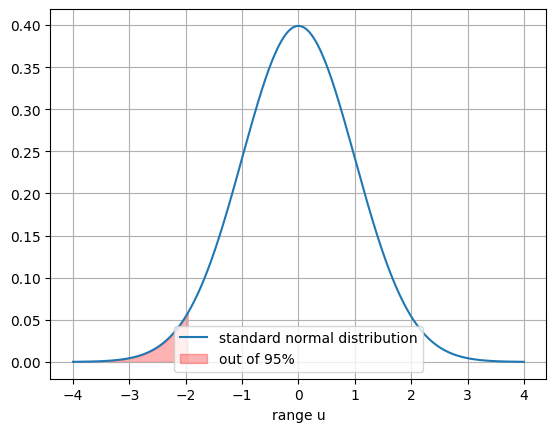
左側検定(5%)

\(-1.645≧u_0\)の時有意

帰無仮説\(H_0\)は棄却される

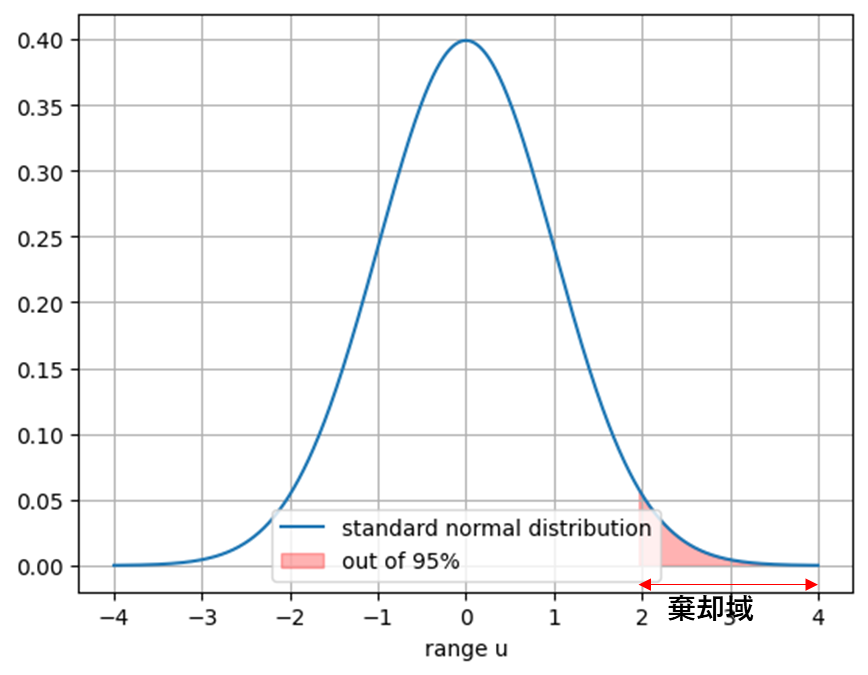
右側検定(5%)

\(1.645≦u_0\)の時有意

帰無仮説\(H_0\)は棄却される

参考文献

まとめ