今回は1標本の
母集団の平均の
検定と推定の
方法を説明致します!
R]※本サイトにはプロモーションが含まれています
目次
1つの母平均に関する検定
1標本の母平均に関する検定は
通常、t検定やZ検定が使われます
これらの検定は
標本から計算された
統計量(t値またはZ値)を基に
母集団の平均がある特定の値と
等しいかどうかを評価します。
| 1つの母平均に関する検定 | 検定 | 検定統計量 |
| 母分散\(σ_0\)が既知の場合 | z検定 | \(\displaystyle u_0= \frac{\bar x-μ}{σ_0/\sqrt{n}}\) |
| 母分散\(σ_0\)が未知の場合 | t検定 | \(\displaystyle t=\frac{\bar x-μ_0}{\hat σ/\sqrt{n}}\) |
z検定
母分散\(σ_0\)が既知の場合
母平均の検定は
以下のような手順になります
1.検定の方針を決める
2.帰無仮説H0,対立仮説H1を設定する
3.有意水準α決める
4.棄却域Rを決める
5.統計量の計算をする
6.統計量と棄却域を比較し検定の結論を決める
ビンに穴をあける工程がある
ビンの穴の直径が
母平均\(μ_0=20um\)
母分散\(σ_0^2=0.2^2\)
となるように設定されている
より直径を小さくするために
装置の設定を変更した。
ビンの穴の直径のデータは以下である
| No.1 | No.2 | No.3 | No.4 | No.5 | No.6 | No.7 | No.8 | No.9 | No.10 |
| 19.64 | 19.72 | 19.65 | 19.68 | 19.7 | 19.73 | 19.66 | 19.73 | 19.69 | 19.68 |
装置設定変更後も
母分散は一致していると仮定し
統計的仮説検定を利用して
ビンの穴の直径が小さくなっているか評価せよ
z検定の方針を決める
装置の設定を変更したことにより
穴の直径が元の直径より小さくなるか
確認したい
帰無仮説は
\(H_0\):装置の設定変更により穴の直径は変化しない
対立仮説は
\(H_1\):装置の設定変更より穴の直径は小さくなった
よって\(H_1:μ≦μ_0\)と設定し
検定統計量が有意水準の値より小さい場合は
帰無仮説を棄却し対立仮説が成立すると
いう左側検定の方針を立てる
帰無仮説,対立仮説を設定する
\(H_0:μ=μ_0\)
\(H_1:μ≦μ_0\)
有意水準\(α\)を決める
\(α=0.05\)とする
棄却域Rを決める
\(u_0≦-1.645\)
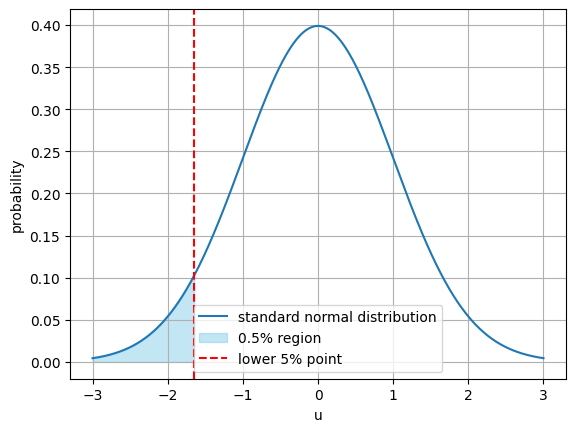
Z検定の検定統計量を計算
\(\displaystyle u_0= \frac{\bar x-μ}{\sqrt{σ_0^2/n}}\)
\(\displaystyle u_0= \frac{19.64-20}{\sqrt{0.2^2/10}}\)
\(=-4.9\)
検定の結論
\(u_0≦-1.645\)より有意である
\(H_0\)は棄却され
装置の設定は変更されたと考える
\(u_0≦-1.645\)より有意である
\(H_0\)は棄却され
装置の設定を変更したことにより
直径は小さくなると判断する
z検定の点推定,区間推定
母平均μの推定手順(σ既知)
点推定:\(\hat μ = \bar x\)
区間推定:信頼率95%の区間μの信頼区間
\((\bar x -1.96 \sqrt{σ_0^2/n} , \bar x +1.96 \sqrt{σ_0^2/n})\)
信頼率99%,90%にしたい時は2.576,1.645とする
点推定:\(\hat μ = \bar x=19.69\)
区間推定:信頼率95%の区間は計算より\((19.56,19.81)\)
t検定

母分散が既知の場合は
z検定を使って検定を
行いますが
実用的な世界では
母分散が未知の場合が
通常です
そういった時はt検定を
利用して検定を
行います
母分散が未知の場合は
与えられたデータから分散を推測して
検定を行う必要がある
標本分散は
\(\displaystyle \hat σ^2=\frac{1}{n-1}\sum_{i=1}^{n}(x_i-\bar x)^2\)
の計算を利用して求めることが出来ます
検定に利用する統計量はtはz検定の統計量uの
母分散\(σ\)から標本分散\(\hat σ\)に置き換えればよい
t検定時の検定統計量tは
\(\displaystyle t=\frac{\bar x-μ_0}{\hat σ/\sqrt{n}}\)で
自由度n-1のt分布に従う

さっきの例題を
母分散が分からない
バージョンで
検定を行います
ビンに穴をあける工程がある
ビンの穴の直径が
母平均\(μ_0=20um\),母分散\(σ_0^2=0.2^2\)
となるように設定されている
より直径を小さくするために
装置の設定を変更した。
ビンの穴の直径のデータは以下である
| No.1 | No.2 | No.3 | No.4 | No.5 | No.6 | No.7 | No.8 | No.9 | No.10 |
| 19.64 | 19.72 | 19.65 | 19.68 | 19.7 | 19.73 | 19.66 | 19.73 | 19.69 | 19.68 |
装置の設定変更後の装置の母分散は未知である。
統計的仮説検定を利用して
ビンの穴の直径が小さくなっているか評価せよ
帰無仮説,対立仮説を設定する
\(H_0:μ=μ_0\)
\(H_1:μ≦μ_0\)
有意水準\(α\)を決める
\(α=0.05\)とする
棄却域Rを決める
tの自由度9下側5%点はt分布表より
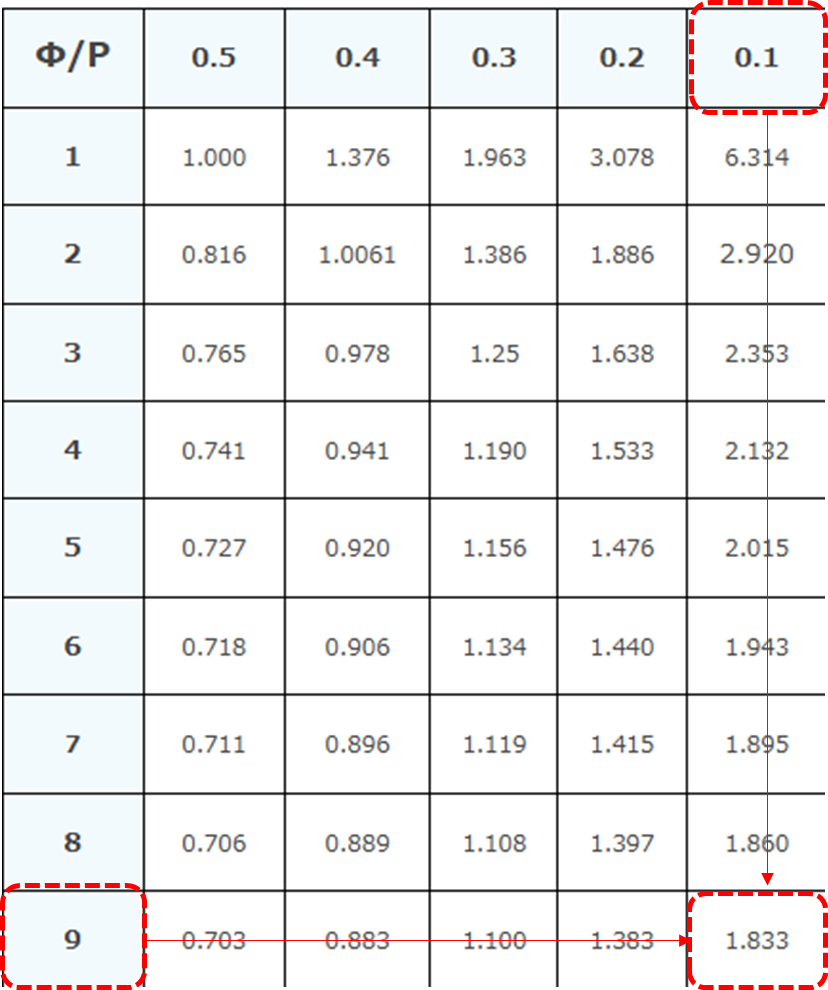
\(t(9,0.1)=1.83\)
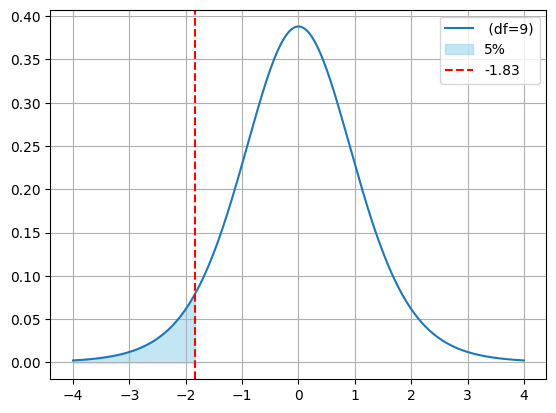
左側検定より棄却域は
\(t≦-t(9,0.1)=-1.83\)
t検定の統計検定量を計算
\(\displaystyle t=\frac{\bar x-μ_0}{\hat σ/\sqrt{n}}\)
\(\bar x=19.688, \hat σ^2=0.00104,σ=0.032,μ_0=20\)
t=-30.83
検定の結論
\(t≦-t(9,0.1)=-1.83\)
より有意である\(H_0\)は棄却され
装置の設定は変更されたと考える
t検定の点推定,区間推定
母平均μの推定手順(σ未知)
点推定:\(\hat μ = \bar x\)
区間推定:信頼率95%の区間μの信頼区間
\((\bar x -t(Φ,α) \sqrt{σ_0^2/n} , \bar x +t(Φ,α) \sqrt{σ_0^2/n})\)
点推定:\(\hat μ = \bar x=19.69\)
区間推定は計算をすると
\(t=19.688±t(9.0.05)・\frac{0.032}{\sqrt{10}}\)
t分布表より\(t(9,0.05)=2.26\)
\(t=19.688±2.26・\frac{0.032}{\sqrt{10}}\)
区間推定:信頼率95%の区間は計算より\((19.66,19.71)\)
参考文献


第4章 母平均に関する検定より