R]※本サイトにはプロモーションが含まれています
・第一種の誤りと第二種の誤りについて知りたい
・検出力について知りたい
・検出力の計算方法について知りたい
・検出力曲線について知りたい
目次
統計的仮説検定の誤り
統計的仮説検定を行う際
帰無仮説\(H_0\)と
対立仮説\(H_1\)を設定する
統計的仮説検定は
母集団から数少ないデータを
サンプリングして推定するものなので
当然誤る可能性がある
検定において2種類の誤りが考えられる。
| (列:検定結果,行:真の結果) | \(H_0\) | \(H_1\) |
| \(H_0\) | 真 | 第二種の過誤 (\(β\)) |
| \(H_1\) | 第一種の過誤\(α\) | 真(\(1-β\)) |
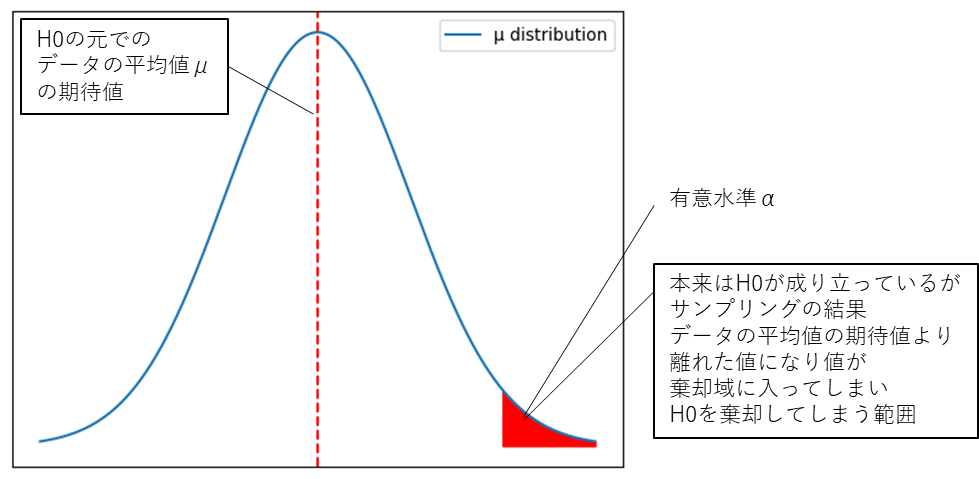
1種の過誤(type I error)
‘本来は帰無仮説\(H_0\)が成り立っているのに
これを棄却してしまう誤り’
これを第一種の過信という
例えば
帰無仮説 : 装置の設定値10umからズレていない
\(H_0\)が正しいのに
棄却し
対立仮説 : 装置の設定値10umからズレている
としてしまう確率である
この誤りを起こす確率は有意水準\(α\)に等しい

もう一つの誤りに
ついて紹介します
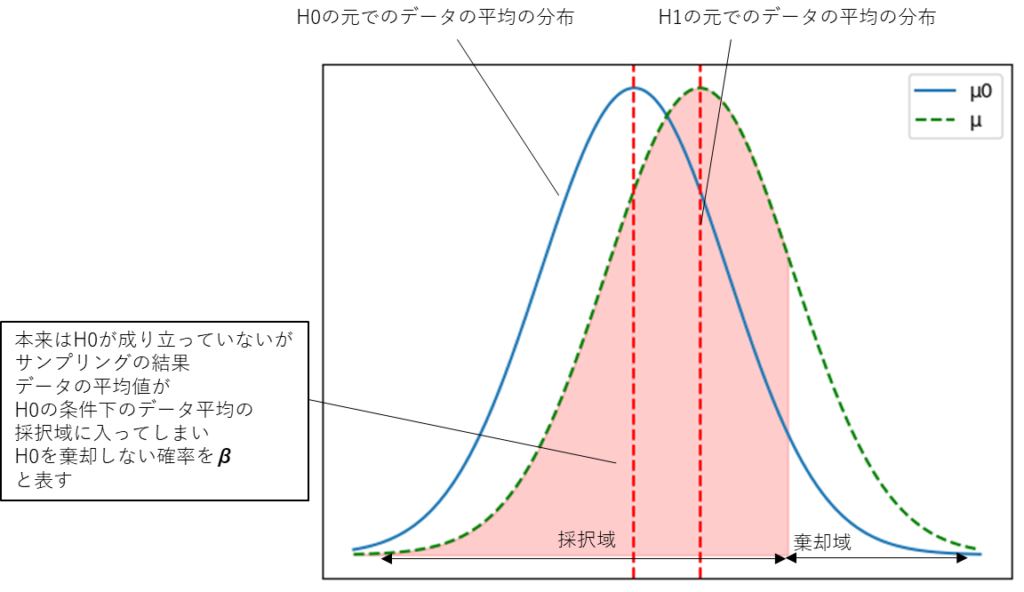
第二種の過誤(type Ⅱ error)
帰無仮説\(H_0\)が
成り立っていないにも関わらず
\(H_0\)を棄却しない誤り
これを第二種の過信という
例えば
帰無仮説 : 装置の設定値10umからズレていない
\(H_0\)が正しくないのに
棄却しない確率である
この誤りを起こす確率をβと表す

がっつり
採択域に
入っちゃってるね!
検出力
検出力とは
帰無仮説\(H_0\)が成り立っていない時
\(H_0\)を棄却する確率
で\(1-β\)で表す
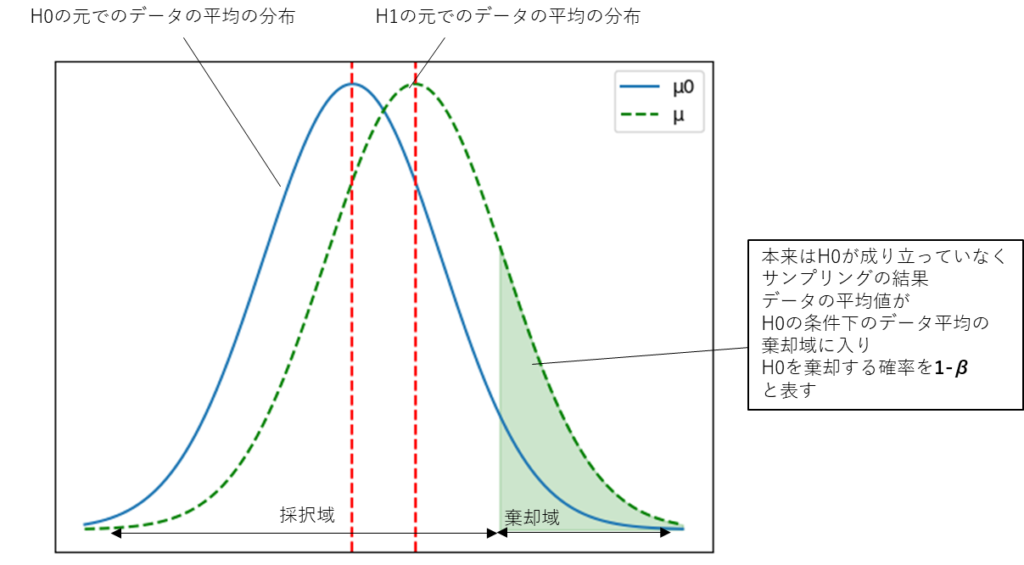
\(μ\)が\(μ_0\)に近い場合
検出力とは
帰無仮説\(H_0\)が成り立っていない時
\(H_0\)を棄却する確率で\(1-β\)で表す
両側検定を考えると
\(H_0:μ=μ_0\)
\(H_1:μ\neq μ_0\)
\(α=0.05\)
統計量\(\displaystyle u=\frac{\bar x-μ_0}{\sqrt{σ_0^2/n}}\)
\(❘u_0❘≧1.96\)なら\(H_0\)を棄却するので
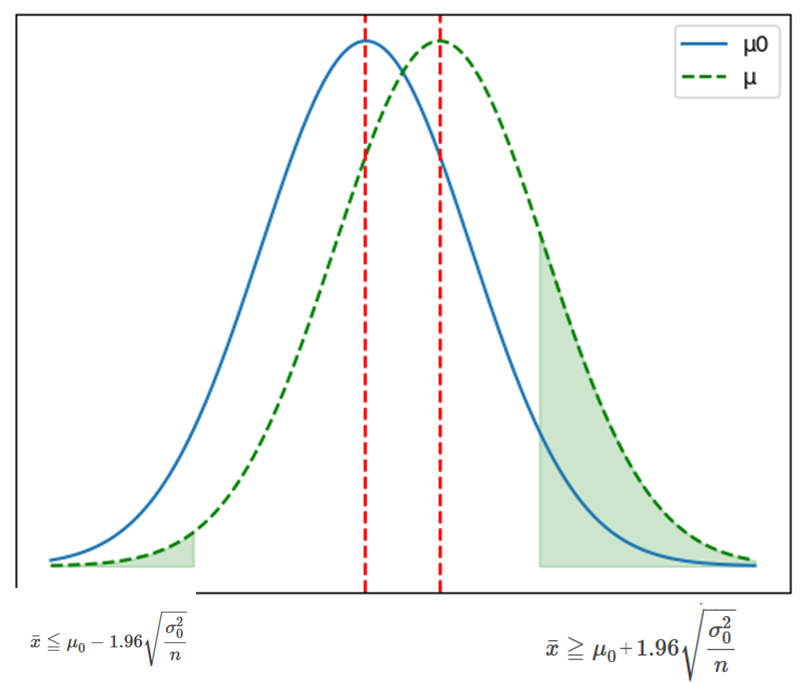
\(\bar x\)の棄却域に変換すると
\(\displaystyle \bar x ≦μ_0-1.96\sqrt{\frac{σ_0^2}{n}}\)
\(\displaystyle \bar x ≧μ_0+1.96\sqrt{\frac{σ_0^2}{n}}\)
検出力1-βは”\(H_1\)が正しい時に
\(H_0\)を採択する確率なので
斜線部以外が第二種の過信βである
MがM0より離れている場合の検出力
\(1-β\)は大きく最大1になる
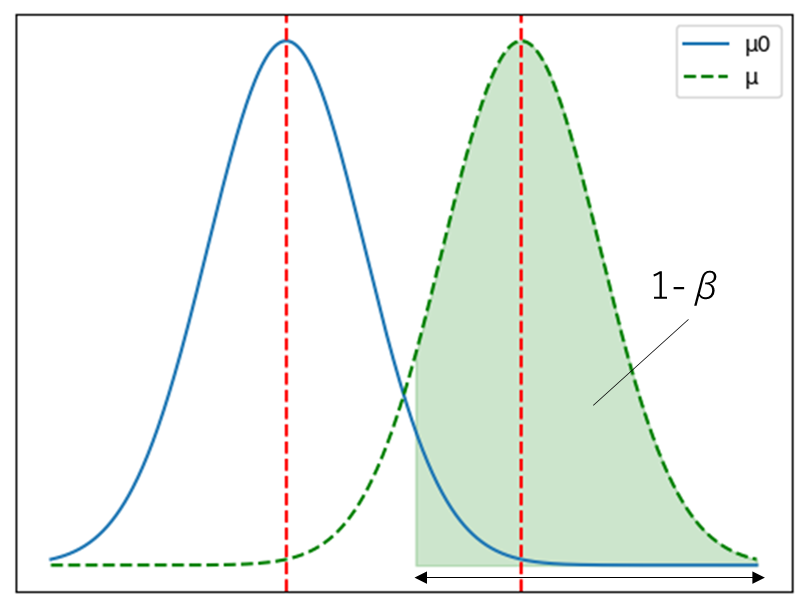

設定値\(μ_0\)より離れているとより
\(H_0\)棄却できる確率が上がるのは
直感的に分かりそうですね
検出力曲線
帰無仮説\(H_0\)が成り立っていない時
\(H_0\)を棄却する確率
\(\displaystyle1-β=Pr(\bar x ≦μ_0-1.96\sqrt{σ_0^2/n})+Pr(\bar x ≧μ_0+1.96\sqrt{σ_0^2/n})\)
uで変換すると
\(\displaystyle=Pr(u≦\sqrt{n}・\frac{μ_0-μ}{σ_0} -1.96)\)
\(+Pr(u≧\sqrt{n}・\frac{μ_0-μ}{σ_0}+1.96)\)
\(\displaystyle \frac{μ_0-μ}{σ_0}\)とサンプルサイズn
が決まれば検出力を求めることが出来る
この式から描かれた曲線を検出力曲線という
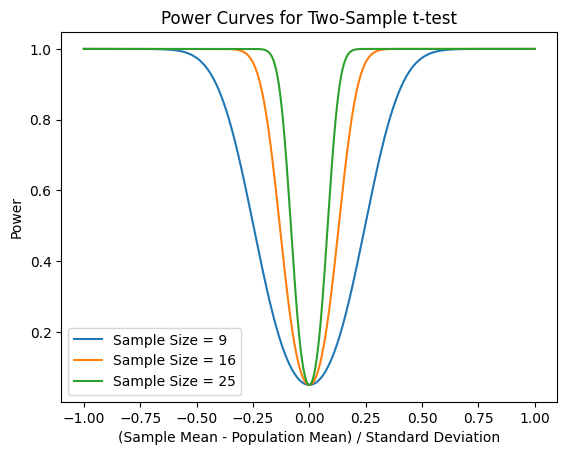
検出力の計算
\(H_0:μ=μ_0\)
\(H_1:μ≧μ_0\)とする
\(\displaystyle \frac{❘μ_0-μ❘}{σ_0}≧1\)の時
高い確率で検出したいと考える
\(\displaystyle \frac{❘μ_0-μ❘}{σ_0}=1\)の際
検出力が\(1-β=0.9\)とするためには
データサイズ(標本数)をどのように設定すればよいか
\(\displaystyle 1-β=Pr(u≦\sqrt{n}・\frac{μ_0-μ}{σ_0} -1.96)\)
\(+Pr(u≧\sqrt{n}・\frac{μ_0-μ}{σ_0}+1.96)\)の
第二項を無視して計算すると
\(Pr(u≦\sqrt{n-1.96}))=0.9\)
確率分布表 より

\(\sqrt{n}-1.96=1.282\)
\(n≒11\)

検出率の計算を行えば
第二種の過信が起こらないように
サンプル数を
コントロール出来るんだ~
参考文献


第三章 検定と推定の
考え方 3.1 ~3.3より