
今回は正規分布と
標準正規分布
正規分布表の
見方を説明します
[PR]※本サイトにはプロモーションが含まれています
目次
連続確率分布とは?
測定値から作られるデータを
連続確率変数と呼ぶ
連続確率変数から
作られる確率分布が
連続確率分布である
連続確率分布の代表的なモデルは
正規分布である。
正規分布はヒストグラムから拡張できる
この記事を参照してください
平均値0ばらつき1の元の
連続変数から作られる確率分布は以下の図になります
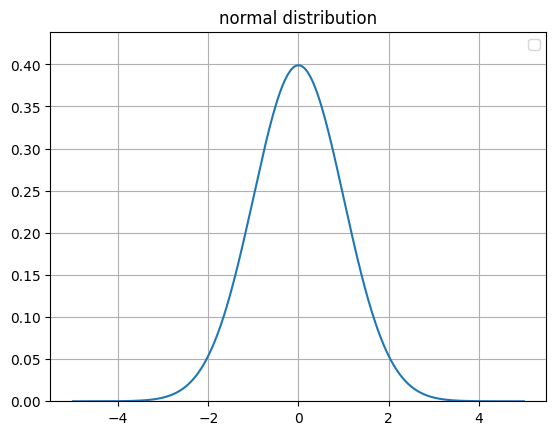

正規分布の特徴を
表す統計量は
尖度と歪度です
平均値分散などです
正規分布(Normal distribution)とは?
工場でモノを作っているとき
どんなに正確にモノを
作ったとしても製品の特性
大きさに関してばらつきが生じる
工程が安定状態の時
測定回数を無限回にし
測定値から確率分布を確認すると
確率分布は「釣鐘型」になります
この曲線を正規分布(Normal Distribution)と言います
この曲線を確率密度関数 \(f(x)\)と呼ぶ
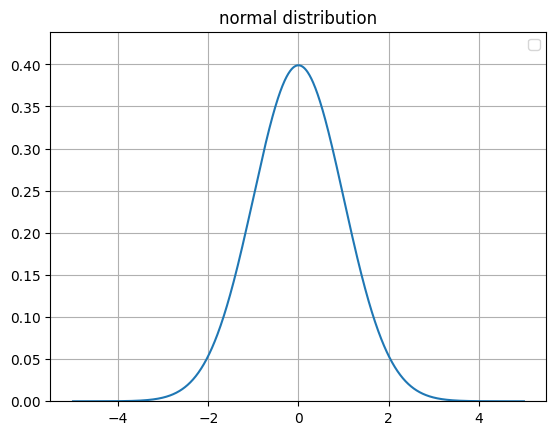
正規分布の確率密度関数は
\(\displaystyle f(x)= \frac{1}{\sqrt{2π}σ}exp[-\frac{1}{2σ^2}(x-μ)^2]\)
\((-∞<x<∞,σ>0)\)

記号を
説明します
| 記号 | 記号の名前 | 記号の種類 |
| \(μ\) | 母平均 | ∞回測定したデータの平均 |
| \(σ\) | 母分散 | ∞回測定したデータの分散 |
正規分布\(f(x)\)は
連続確率分布なので以下の性質が成り立つ
\(\displaystyle \int_{-∞}^∞ f(x)dx=1\)
区間(a≦x≦b)の確率Pr
\(\displaystyle P_r(a≦x≦b)=\int_{a}^b f(x)dx\)
期待値
\(E(x)=\displaystyle x\int_{-∞}^∞ f(x)dx\)
正規分布(Normal distribution)の特徴
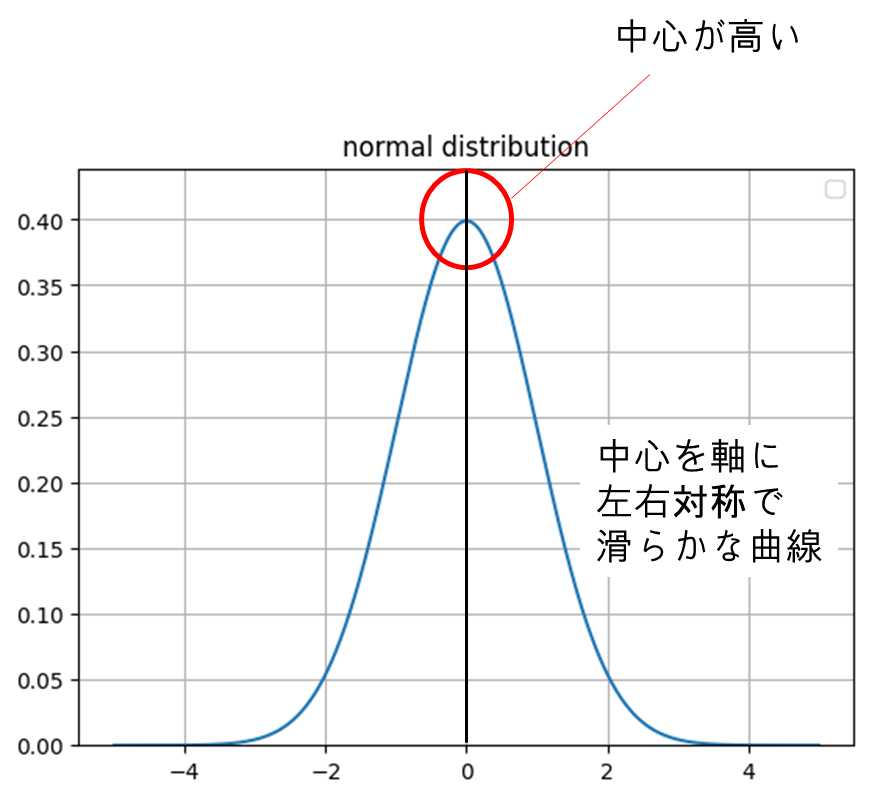
鐘型曲線
正規分布の確率密度関数は
中心が最も高く
左右対称の滑らかな曲線を描きます
この形状から「ベルカーブ」とも呼ばれます
平均と分散
正規分布は平均(μ)と分散(σ²)で完全に決定されます
平均は分布の中心位置を示し
分散はデータのばらつき具合を示します。
\(\displaystyle f(x)= \frac{1}{\sqrt{2π}σ}exp[-\frac{1}{2σ^2}(x-μ)^2]\)

式を見ると
正規分布は
母平均と
母分散で
決まってることが
わかるね!
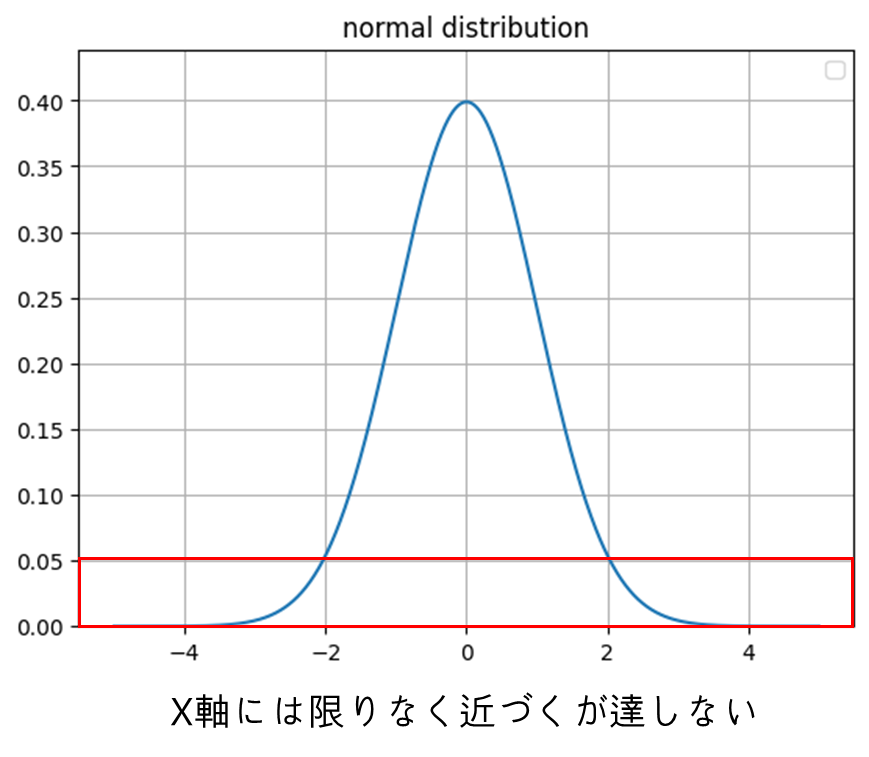
対称性
正規分布の両端は無限に伸びていますが
x軸に漸近しており
決してx軸に達しません
つまり理論的には
どんなに離れた値も存在する可能性がありますが
その確率は非常に低くなります。
正規分布の特徴を表現する統計量
平均、分散、歪度、尖度は正規分布を表す統計量です
各統計量に関してはこちらの記事を
参照ください
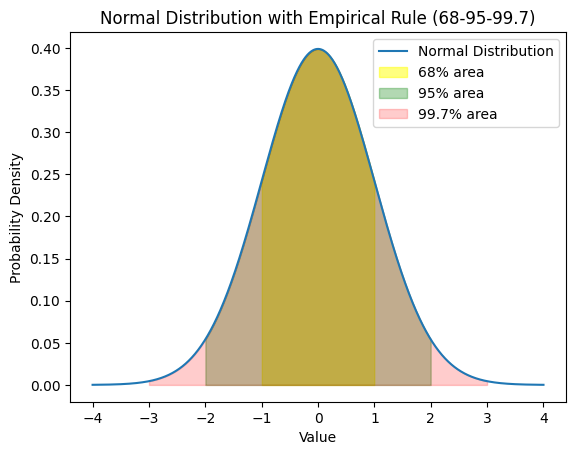
エンピリカルルール
正規分布では
データの約68%が平均から
±1標準偏差の範囲内に
約95%が±2標準偏差の範囲内に
約99.7%が±3標準偏差の範囲内に存在します。
中心極限定理
中心極限定理によれば
充分に大きなサンプルサイズを持つ
独立同分布のランダム変数の和は
正規分布に近似されます。
このため
正規分布は多くの実際のデータ解析で利用されます。
標準正規分布
正規分布は平均値と標準偏差が分かれば
ある区間の確率を知ることが出来る
しかしある区間の確率を求めるには
平均値と標準偏差ごとに形成される
正規分布の面積を求めなくてはならない
そこで簡単にある区間の確率を
計算するために基準となる正規分布を
標準正規分布という
統一された標準正規分布で解析を行うために
正規分布を平均値0標準偏差1の
標準正規分布に変換する
操作のことを標準化と言います
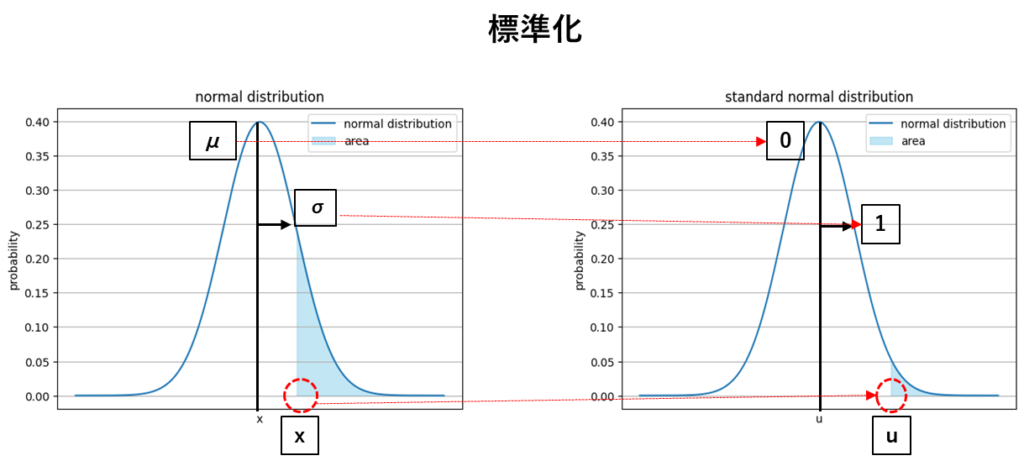
標準化の方法
標準化は
確率変数xをuに変換する操作のことである
\( \displaystyle u=\frac{x-μ}{σ}\)
\(確率変数uはN(0,1^2)に従う\)
標準確率密度関数
\(\displaystyle f(Z)= \frac{1}{\sqrt{2π}}exp[-\frac{u^2}{2}]du\)

正規分布を
標準化すると
正規分布度表を
利用して
ある区間の
確率を求める
ことが出来るように
なります!
正規分布表を使って区間確率を求める
確率変数xを標準化した
確率変数uと\(N(0,1^2)\)の
正規分布表を活用して
区間確率を求めていきます
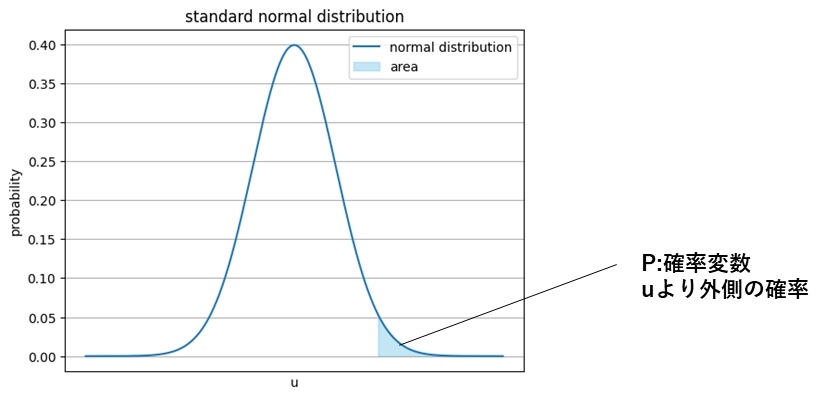
正規分布表とは
正規分布表Ⅰとは
標準化した値 uより外側の確率を表した表です。
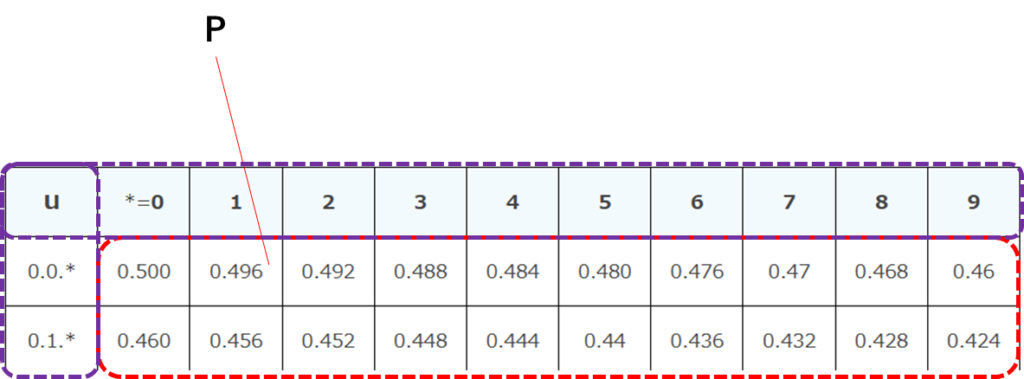
正規分布表Ⅰを利用してuの値から確率Pを求める
u=1.5の時の確率Pr(Z≧1.5)は?
正規分布表Ⅰからu=1.5の点を探す
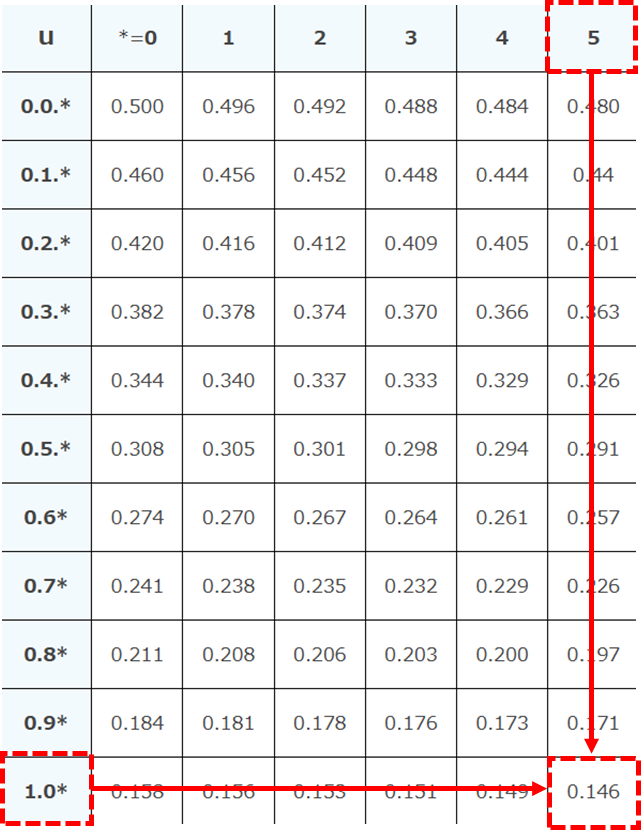
u=1.5の時正規分布表よりP(Z≧1.5)=0.146
- u=1.65の時の確率Pr(Z≧1.65)は?
- u=1.96の時の確率Pr(Z≧1.96)は?
正規分布表Ⅱを利用してuの値から確率Pを求める
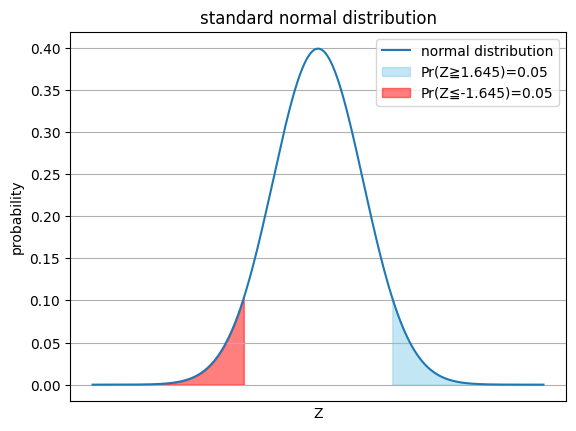
Pr(Z≧u)=0.05の時の確率変数uは?
Pr(Z≦u)=0.05の時の確率変数uは?

P=0.05の時、正規分布表Ⅱより
Pr(Z≧u)=0.05の時の確率変数uはu=1.645
正規分布は左右対称の釣鐘型の分布より
Pr(Z≧u)=0.05の時の確率変数uはu=ー1.645
Pr(Z≧u)=0.05の時の確率変数uはu=1.645
Pr(Z≦u)=0.05の時の確率変数uはu=ー1.645
正規分布表を利用した実践例題
ある装置で一日に
10,000個パンを作っていました
工程が安定状態の時
この装置を利用してパンを作ると
重さが100gで
標準偏差が4の正規分布に基づいた
重さのパンが出来上がることが分かっています
この企業では90g以下のパンは規格外として
売らないようにしています。
一日に10,000個パンを作るとき
規格外品は何個できるでしょうか?
確率変数xはパンの重さ(g)です
測定値x=90(g)とします
次に確率変数xをuに標準化していきます。
\(\displaystyle u=\frac{x-μ}{σ}\)より
\(\displaystyle u=\frac{90-100}{4}\)
\(u=-2.5\)
u=-2.5の時の正規分布表を確認すると
確率分布表 | データと統計学 (df-learning.com)
Pr(Z≦-2.5)=0.006
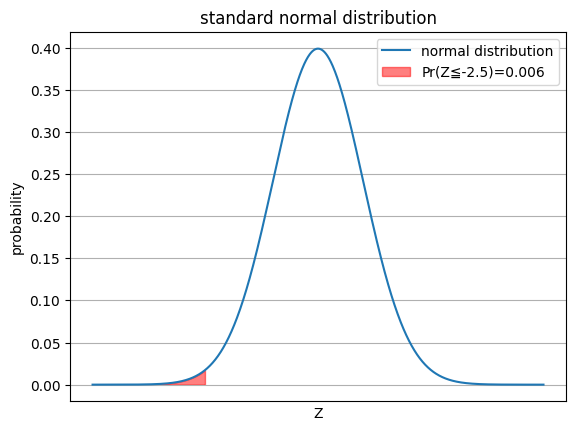
売れないパンが出来る確率はP=0.006つまり6%
一日に10,000個パンを作るとき
規格外品の数は
=10,000×0.006=60
一日に10,000個パンを作るとき規格外品の数は60個発生する可能性が高い


