
あい
今回はカイの二乗分布に
ついて解説していきます
[PR]※本サイトにはプロモーションが含まれています
カイの二乗分布
確率変数\(Z_1,Z_2,…..Z_3\)が
互いに独立に\(N(0,1)\)に従う時
\(W = Z_1^2 + Z_2^2 +…+ Z_n^2\)
は\(X^2\)分布に従う
期待値と分散は
\(E[W] = n , V[W] =2n\)
カイの二乗分布の性質を
いくつか紹介します
2つの確率変数\(W_1 , W_2\)が独立に\(X^2(m_1),X^2(m_2)\)に従う時
\(W_1 + W_2\)は\(X^2(m_1 +m_2)\)に従う
標本\(X_i\)が母集団\(N(μ,σ^2)\)に従う時
\(\displaystyle W =\sum_{i=1}^{n}\frac{(x_i-μ)^2}{σ^2}\)
は自由度nの\(x^2\)分布に従う
標本\(X_i\)が母集団\(N(μ,σ^2)\)に従う時
\(\displaystyle W =\sum_{i=1}^{n}\frac{(x_i-\bar x)^2}{σ^2}=\frac{(n-1)S^2}{σ^2}\)
は自由度n-1の\(x^2\)分布に従う
自由度1,3,5,10のxの二乗分布
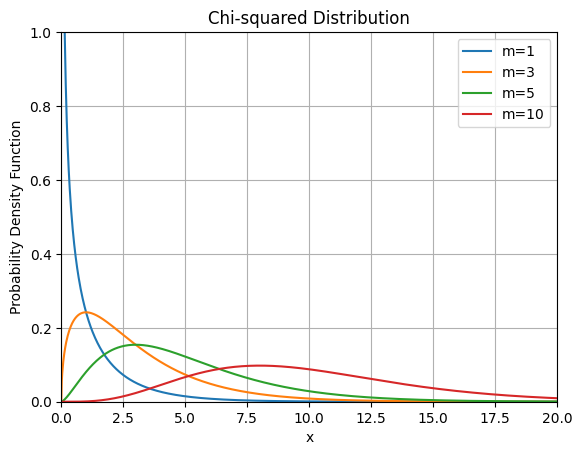

あい
面白い分布になりますね!
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import chi2
# 自由度
degrees_of_freedom = [1, 3, 5,10]
# x軸の値
x = np.linspace(0, 20, 1000)
# 各自由度ごとに確率密度関数を計算
for Φ in degrees_of_freedom:
y = chi2.pdf(x, Φ)
plt.plot(x, y, label=f'Φ={Φ}')
# グラフの設定
plt.title('Chi-squared Distribution')
plt.xlabel('x')
plt.ylabel('Probability Density Function')
plt.legend()
# x軸の範囲を設定して0点を左端に
plt.xlim(0, 20)
# y軸の範囲を設定して0点を下端に
plt.ylim(0, 1)
plt.grid(True)
plt.show()\(χ^2\)表の見方
例題
\(x^2(10,0.05)\)を\(x^2表\)
を利用して値を求めよ
確率分布表 | データと統計学 (df-learning.com)
\(x^2\)表からP=0.05,Φ=10が交わる点を確認すると
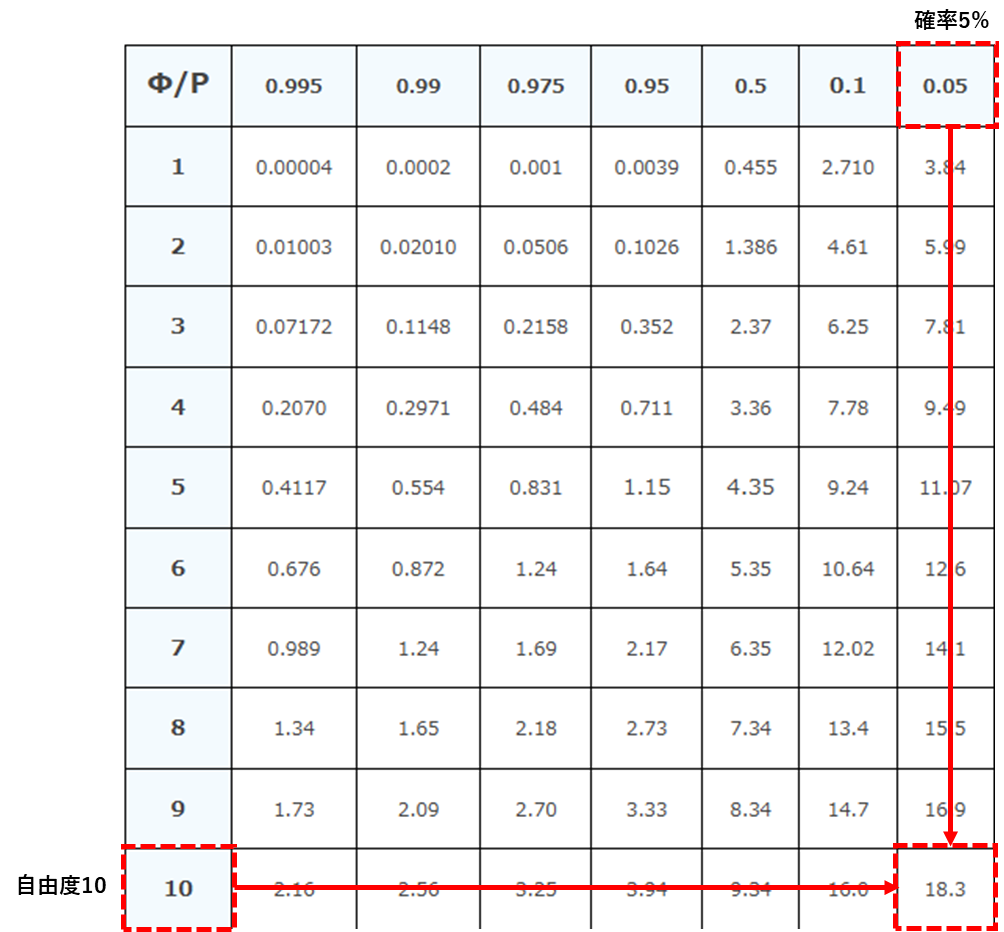
答え
\(x^2(10,0.05)=18.3\)
参考文献

日本統計学会公式認定
統計検定2級対応
統計学基礎

あい
2章確率と確率分布より


