あい
今回はR言語を
利用して1標本の
母集団に関する
検定と推定を
行うプログラムを
実装します
R]※本サイトにはプロモーションが含まれています
R言語とは?
R言語は、統計解析やデータ可視化のために
設計されたプログラミング言語および環境です
Rは、様々な統計手法
をサポートしています

あい
早速検定を
やっていきましょ~
t検定
例題2
ビンに穴をあける工程がある
ビンの穴の直径が
母平均\(μ_0=20um\),母分散\(σ_0^2=0.2^2\)
となるように設定されている
より直径を小さくするために
装置の設定を変更した。
ビンの穴の直径のデータは以下である
| No.1 | No.2 | No.3 | No.4 | No.5 | No.6 | No.7 | No.8 | No.9 | No.10 |
| 19.64 | 19.72 | 19.65 | 19.68 | 19.7 | 19.73 | 19.66 | 19.73 | 19.69 | 19.68 |
装置の設定変更後の装置の母分散は未知である。
統計的仮説検定を利用して
ビンの穴の直径が小さくなっているか評価せよ
t検定を実装する
データをcsvに格納します
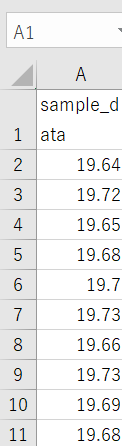
データをcsvから読み込む
# データの読み込み
sample_data <- read.csv("sample_data.csv")
# データを確認する
print(sample_data)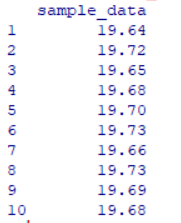
検定の計算を行うためにベクトル変換します
sample_data <- sample_data[[1]]
print(sample_data)
帰無仮説の平均\(μ=20um\)
有意水準\(α = 0.05\)
# 検定の設定
mu <- 20 # 仮定の母平均
alpha <- 0.05 # 有意水準
n <- length(sample_data) # サンプルサイズ標本平均と
母分散は未知なので
標本標準偏差の計算をする
# 標本平均と標本標準偏差の計算
sample_mean <- mean(sample_data)
sample_sd <- sd(sample_data)統計量tの計算をする
# 統計量tの計算
t_statistic <- (sample_mean - mu) / (sample_sd / sqrt(n))
# 臨界値の計算
critical_value <- qt(alpha, df = n - 1)検定を行うコードを実装する
if (t_statistic < critical_value) {
result <- "帰無仮説を棄却する"
} else {
result <- "帰無仮説を棄却できない"
}
# 検定結果の表示
cat("検定統計量 (t):", t_statistic, "\n")
cat("臨界値:", critical_value, "\n")
cat("結論:", result, "\n")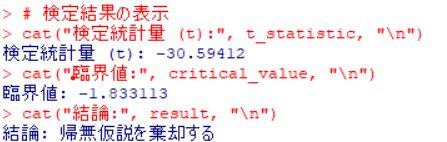
完成しました!
纏めると
# データの読み込み
sample_data <- read.csv("sample_data.csv")
# データを確認する
print(sample_data)
# ベクトルに変換
sample_data <- sample_data[[1]]
print(sample_data)
# 検定の設定
mu <- 20 # 仮定の母平均
alpha <- 0.05 # 有意水準
n <- length(sample_data) # サンプルサイズ
# 標本平均と標本標準偏差の計算
sample_mean <- mean(sample_data)
sample_sd <- sd(sample_data)
# 統計量tの計算
t_statistic <- (sample_mean - mu) / (sample_sd / sqrt(n))
# 臨界値の計算
critical_value <- qt(alpha, df = n - 1)
if (t_statistic < critical_value) {
result <- "帰無仮説を棄却する"
} else {
result <- "帰無仮説を棄却できない"
}
# 検定結果の表示
cat("検定統計量 (t):", t_statistic, "\n")
cat("臨界値:", critical_value, "\n")
cat("結論:", result, "\n")
あい
できました~
点推定と信頼区間95%の区間推定を行う
下記コードを追加してください
# 点推定
point_estimate <- sample_mean
# 95%信頼区間の計算
t_critical <- qt(1 - alpha / 2, df = n - 1) # 95%信頼区間のt値
margin_of_error <- t_critical * (sample_sd / sqrt(n))
confidence_interval <- c(point_estimate - margin_of_error, point_estimate + margin_of_error)
# 点推定と信頼区間の表示
cat("点推定:", point_estimate, "\n")
cat("95%信頼区間: [", confidence_interval[1], ", ", confidence_interval[2], "]\n")