あい
今回はpythonを使って
ポアソンモデルの
例題を計算
次にポアソン分布を
表示するプログラムを
pythonで実装します
[PR]※本サイトにはプロモーションが含まれています
ポアソン分布のモデル
ポアソン分布は
ポアソン分布とは二項分布の確率分布で
nが限りなく大きい場合の極限分布です。
二項分布はベルヌーイ試行(成功 or 失敗)
をN回行ってx回成功した確率を
表す確率分布です
二項分布は以下の式で表します
\(P_r(X=x)=nC_xP^x(1-P)^{n-x}\)
ポアソン分布は
\(np = λ\)と置き
\(n→∞ , p→0\)とし
以下の式に変換されます
\(\displaystyle P_r(X=x)=\frac{λ^2}{x!}e^{-λ}\)
ポアソンモデルの例題を準備
例題
50万回メモリの書き込みを行うと
1回は書き込みエラーが発生する
USBメモリが存在する
25万回で2個故障が
発生する確率をポアソン分布を
利用して求めよ
USBメモリが1回の書き込みでエラーが発生する確率P
\(\displaystyle P=\frac{1}{500,000}\)
\(P=0.000002\)
\(λ=nP\)より
\(λ=250000*0.000002\)
\(λ=0.5\)
次に\(\displaystyle P_r(X=x)=\frac{λ^2}{x!}e^{-λ}\)
の計算をpythonで行います
poisson_pmf = poisson.pmf(x, lambda_parameter)このコードで故障確率を計算することが出来ます
そしてλ = 0.5 , X =2を入れて以下のコードを描くと
2回故障する確率を計算してくれます
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import poisson
λ = 0.5
x = np.arange(0,11)
X =2
poisson_pmf = poisson.pmf(x, λ)
for i , z in zip(x,poisson_pmf):
if i == X:
print("メモリの書き込みが25万回行われたとき2回故障する確率は",z)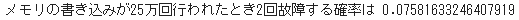

あい
おおよそ故障確率は
7.6%だね!
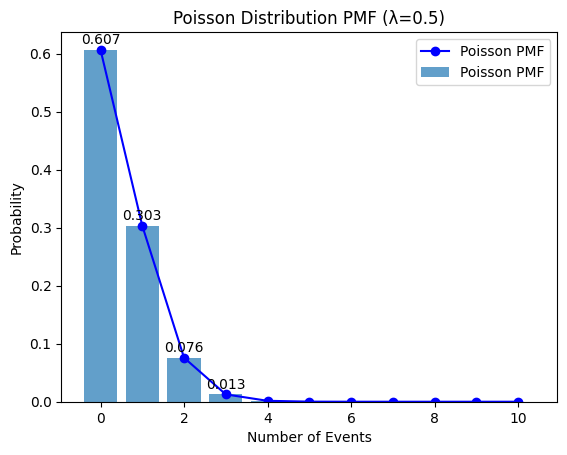
このモデルのポアソン分布を見てみる
最後に以下のコード追加して
ポアソン分布を折れ線と棒グラフにして
観察してみます
plt.bar(x, poisson_pmf, align='center', alpha=0.7, label='Poisson PMF')
plt.plot(x, poisson_pmf, marker='o', label='Poisson PMF', linestyle='-', color='b')
plt.title('Poisson Distribution')
plt.xlabel('Number of Events')
plt.ylabel('Probability')
plt.title('Poisson Distribution PMF (λ={})'.format(λ))
# 上位4つの要素のインデックスを取得
top_indices = np.argsort(poisson_pmf)[::-1][:4]
# 各バーの上に確率値を表示
for i in top_indices:
plt.text(x[i], poisson_pmf[i] + 0.01, f'{poisson_pmf[i]:.3f}', ha='center')
plt.legend()
plt.show()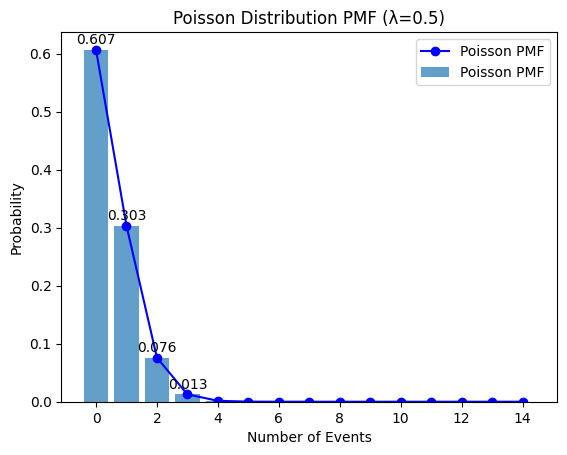
コードのまとめ
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import poisson
λ = 0.5
x = np.arange(0,11)
X =2
poisson_pmf = poisson.pmf(x, λ)
for i , z in zip(x,poisson_pmf):
if i == X:
print("メモリの書き込みが25万回行われたとき2回故障する確率は",z)
plt.bar(x, poisson_pmf, align='center', alpha=0.7, label='Poisson PMF')
plt.plot(x, poisson_pmf, marker='o', label='Poisson PMF', linestyle='-', color='b')
plt.title('Poisson Distribution')
plt.xlabel('Number of Events')
plt.ylabel('Probability')
plt.title('Poisson Distribution PMF (λ={})'.format(λ))
# 上位4つの要素のインデックスを取得
top_indices = np.argsort(poisson_pmf)[::-1][:4]
# 各バーの上に確率値を表示
for i in top_indices:
plt.text(x[i], poisson_pmf[i] + 0.01, f'{poisson_pmf[i]:.3f}', ha='center')
plt.legend()
plt.show()