[PR]※本サイトにはプロモーションが含まれています

あい
今回は偏差値に
ついて解説します
合わせて読みたい
偏差値(Standard Score)とは
偏差値とは
データの個々の値が
平均値が50、標準偏差が10の正規分布
の平均値からどれだけ離れているか
を数値にして確認する指標です
データの個々の値の確率変数xを
\(N(50,10^2)\)に従う確率変数に
変換します
\(\displaystyle Z=\frac{X-μ}{σ}×10+50\)

あい
偏差値は
この正規分布の平均値から
どれだけ離れているかを
理解する尺度なんですね!
早速例題を解いて偏差値に対して
理解を深めていきましょう!
例題1
偏差値
数学の全国模試の
平均点が62点
標準偏差が15であった
自身の点数は70点だった
偏差値を計算せよ
\(\displaystyle Z=\frac{70-62}{15}×10+50\)
\(=55.3\)
自身の偏差値は55.3です

あい
真ん中の人より
点数良かったんだ~
偏差値55.3が具体的に上位何%なのか
次の例題で計算します
例題2
偏差値
数学の全国模試の偏差値は55.3点だった
この人のテスト点数は上位何%でしょうか
正規分布表を使って確認せよ
正規分布表はN(0,1)の確率密度関数に
従う表です。
偏差値は\(N(50,10^2)\)の正規分布に
従う確率変数なので
標準化を行う必要がある
\(\displaystyle u=\frac{55.3-50}{10}\)
\(u = 0.53\)
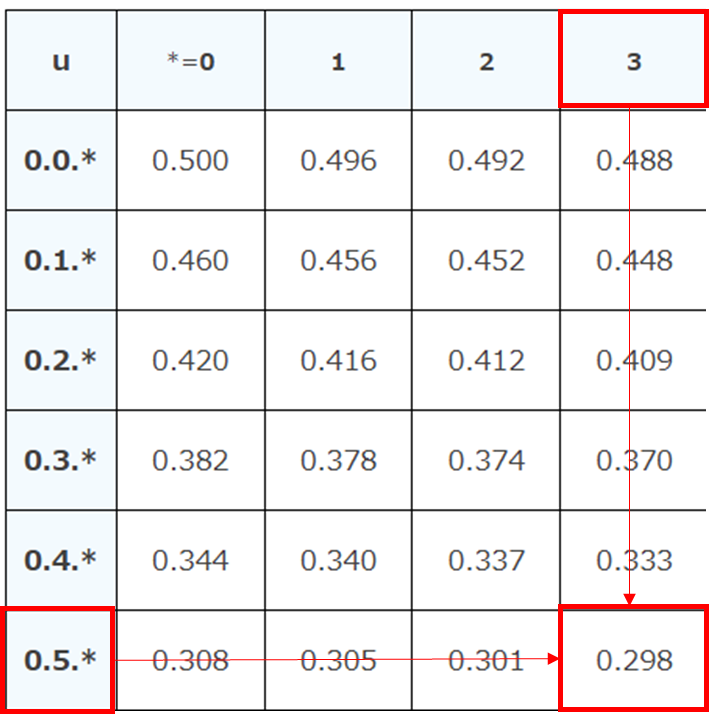
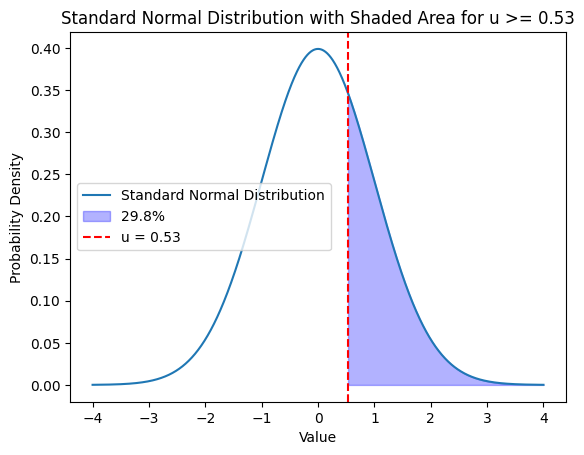
Pr(x≧55.3) = 0.298より
この人の数学の点数は全国模試受験者の中で
上位29.8%であることが分かる