[PR]※本サイトにはプロモーションが含まれています
正規分布の性質
実験や観察などで得られた計量値は
偶然ばらついているのではなく
母集団の正規分布に基づいて現れた値
であると考えることが出来る
与えられた計量値を\(x_1,x_2….x_n\)と置くと
計量値\(x_1,x_2….x_n\)の分布
確率変数\(x_1,x_2…x_n\)が正規分布に
従っているとすれば確率変数xは\(N(μ,σ^2)\)に従う
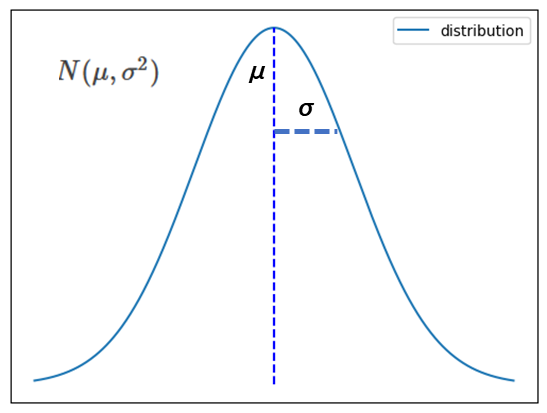
確率変数xが\(N(μ,σ^2)\)に従い,aとbを定数とするとき
\(ax+b\)の分布は
\(N(aμ+b,a^2σ^2)\)
2つの確率変数xとyが独立に
\(N(μ_1,σ_1^2),N(μ_2,σ_2^2)\)に従う時
x + yは
\(N(μ_1+μ_2,σ_1^2+σ_2^2)\)に従う
平均値の確率分布
データは全くでたらめな値を
とっているのではなく
正規分布に基づいて
分布の範囲内でばらついている
と考えるのであれば
データから計算される
平均値も
正規分布のような法則性を持っている
と推定できる
平均値の分布は
\(\bar xはN(μ,\frac{σ^2}{n})\)に従う


