
Yamu
今回はRを利用して
重回帰モデルの分散
分析を行っていきます!
[PR]※本サイトには、プロモーションが含まれています
重回帰モデルの分散分析
分散分析とは
異なるグループ間のばらつきを
比較する統計的手法であり
重回帰分析では
説明変数と目的変数の
関係を評価します。
平方和の成分分解は
「総平方和 = 回帰による平方和 + 誤差による平方和」であり
誤差による平方和は残差の平方和です
分散分析の統計量Fは
回帰の平均平方と誤差の平均平方を使って計算されます
帰無仮説は
すべての回帰係数がゼロである
これを確認することによって
統計的に有意な影響を与えるかどうかを検定します。
Rを利用した重回帰モデル
Rには、経済学のデータセットである
「Longley」が組み込まれています。
これは、アメリカの経済データを元にした
データセットであり、
7つの変数(カラム)から構成されています。
longleyデータセットのカラムは以下の通りです
- GNP.deflator : GNPデフレーター
- GNP : 国民総生産
- Unemployed : 失業者数
- Armed.Force : 軍隊の人数
- Population : 人口
- Year : 年
- Employed : 雇用者数
次のRコードは、longleyデータセットを使ってEmployを目的変数とする
重回帰モデルをステップワイズ法で構築し
その後分散分析を行います。
# longleyデータセットを使用するために読み込みます
data(longley)
# データの先頭の行を表示します
head(longley)
# 雇用者数を目的変数、他の変数を説明変数とした重回帰モデルを最小二乗法で推定します
result <- lm(Employed ~ ., data = longley)
# ステップワイズ法を使用した変数選択を実行します
result.step <- step(result)
# 分散分析を実行し、結果を表示します
anova_result <- anova(result.step)
print(anova_result)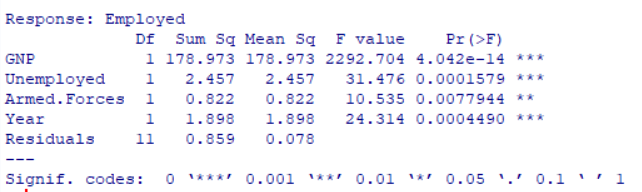
F値とP値を確認すると1%以下の棄却域に
全て入っているので
帰無仮説は棄却でき回帰は有意であると言える


