
今回は重回帰モデルに
ついて説明します
[PR]※本サイトには、プロモーションが含まれています
線形重回帰モデルとは
目的変数 y の値を決める
複数の要因を説明変数 Xとし
線形重回帰モデルを作って
目的変数の予測や説明を行う統計的手法の一つです
重回帰モデルは以下のような形で表されます
\(Y=B_0+B_1X_1+…+B_nX_n+ε\)
\(ε\)は互いに独立に\(N(0,σ^2)\)
Yは目的変数
\(B_0\)は定数項
\(B_1\,B_2….B_n\)は回帰係数
\(X_1\,X_2….X_n\)は独立変数
\(ε\)は誤差項
重回帰モデルの例

ある不動産の価格は
部屋の広さ
築年数
駅からの近さ
部屋の数
など様々な要因で
決定されていると仮定します
これらの要因は価格に影響を及ぼすと
仮定しているので
説明変数\(x_1,x_2,x_3,x_4\)とおきます
そして説明変数の影響を受けている
目的変数Yは
価格になります
回帰係数の推定
線形重回帰モデルでは
切片を含む回帰係数に対応する
パラメータ\(B_0,B_1….,B_n\)を
推定することが必要である
パラメータの推定には
最小二乗法と最尤法がある
最小二乗法では誤差を最小にする回帰係数を求める
ことが基本的な考え方なので
\(\displaystyle S(B_0,B_1….,B_P)=\sum_{i=1}^nε_i^2\)
\(\displaystyle =\sum_{i=1}^n{y_i-(B_0+B_1x_{i1}+・・・+B_px_{ip})}^2\)
各係数に関して偏微分をし
解を0と置いたp+1個の連立方程式
を解くことで
推定量を求めることが出来る
今後は回帰係数は推定値なので
推定量を\(\hat β\)と置き
説明変数の数がn個の時
回帰係数の推定値の値は
p+1次元ベクトル
\(\mathbf{\hat{B}}=(\hat B_0, \hat B_1, …, \hat B_p)\)は
行列\(\mathbf{{(X^TX)^{-1}}}\)が正則であれば
下記の式で導出が可能になる
\(\mathbf{\hat B=(X^TX)^{-1}X^Ty}\)

実際は解析ソフトを
利用して計算するので
読み飛ばして
いただいて結構です
Rで線形重回帰モデルの作成
Rのlgrdataパッケージの
allometryデータを用いる
allometryは松の木に対して
品種(species)
直径(diameter)
樹高(height)
葉面積(leaf area)
枝の重さ(branchmass)
をデータ測定したものである
今回は
枝の重さを目的変数
直径,樹高,葉面積を説明変数とした
線形重回帰モデルをRで構築する

# lgrdataライブラリ読み込み
library(lgrdata)
# 松の木のデータを読み込む
data(allometry)
# 目的変数と説明変数を設定する
fm = branchmass ~ diameter + height + leafarea
# 線形重回帰モデルの実行
res = lm(fml, data = allometry)
#出力
resデータから推定された回帰係数の値が出力される
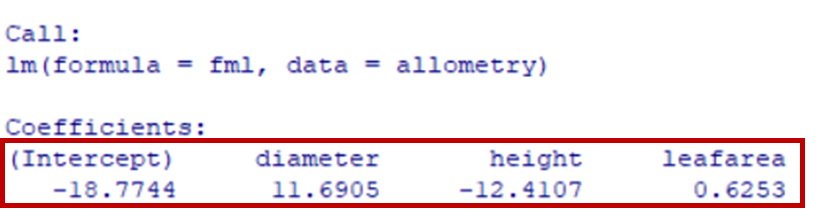
| 切片 | 直径 | 樹高 | 葉面積 |
| -18.77 | 11.69 | -12.41 | 0.63 |
枝の重さ=-18.77+11.69直径-12.41樹高+0.63葉面積
モデルの当てはまりが
悪い場合は適切な予測が出来ない
可能性があるので
モデルの評価も必要に
なってきます
参考文献

(データサイエンス大系)

回帰分析Ⅱ -重回帰モデルより


