こんにちわ!Yamuです
今回はExcelのデータ分析機能
一元配置法を利用して
分散分析を
行っていきます!
[PR]※本サイトには、プロモーションが含まれています
分散分析とは?
分散分析とは、ばらつきを分けて解析する方法です
ある因子の影響によって発生するばらつきが
統計的に有意かどうかを評価するのに役立ちます。
具体的な分散分析の手順を示します。
一元配置法 例題
【分散分析】一元配置法分散分析の実践例 と同じ例題を利用します。
ある農場で、3つの異なる肥料の効果を比較するために
同じ作物を用いて実験が行われました。
各肥料をランダムに選んで
それぞれ10区画に適用しました。
収穫量(kg)が収集され、
肥料の効果を比較するために分散分析を実施します。
| 水準 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 肥料A | 18 | 20 | 22 | 25 | 24 | 21 | 19 | 23 | 20 | 22 |
| 肥料B | 17 | 16 | 18 | 19 | 20 | 21 | 22 | 19 | 18 | 17 |
| 肥料C | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 |
エクセルで分散分析
Excelのデータ分析機能を利用して
一元配置分散分析を行います。
データをセット
エクセルにデータをセットします。

データ分析から一元配置を選択
データからデータ分析を選択

データ分析から分散分析 : 一元配置を選択
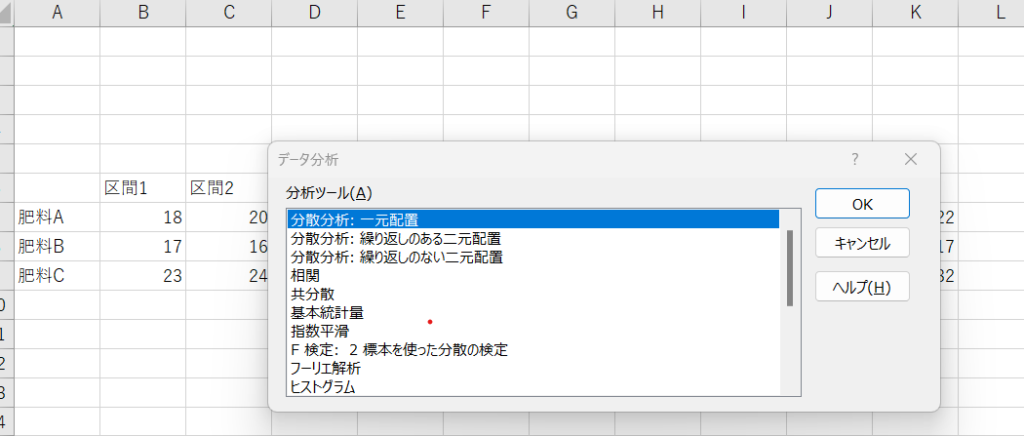
入力範囲にデータの範囲はB7からK9
データ方向に水準内の繰り返しは行を
入力する
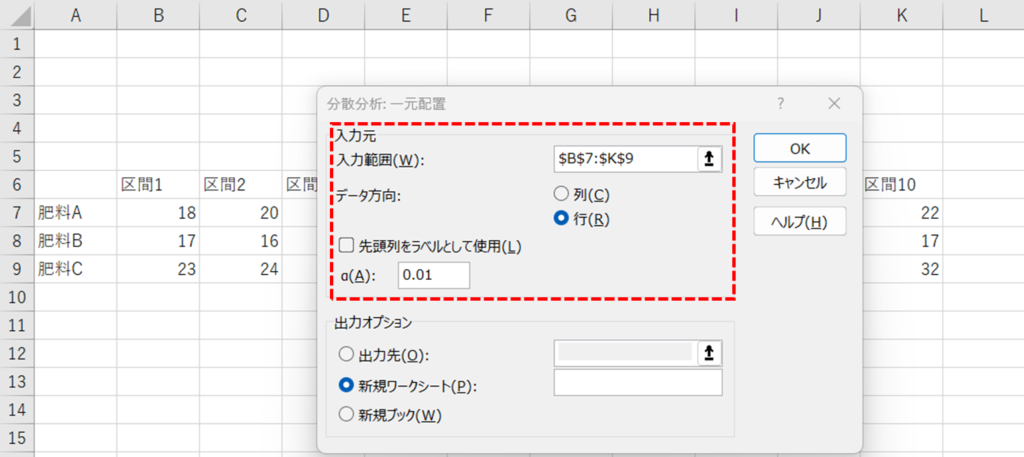
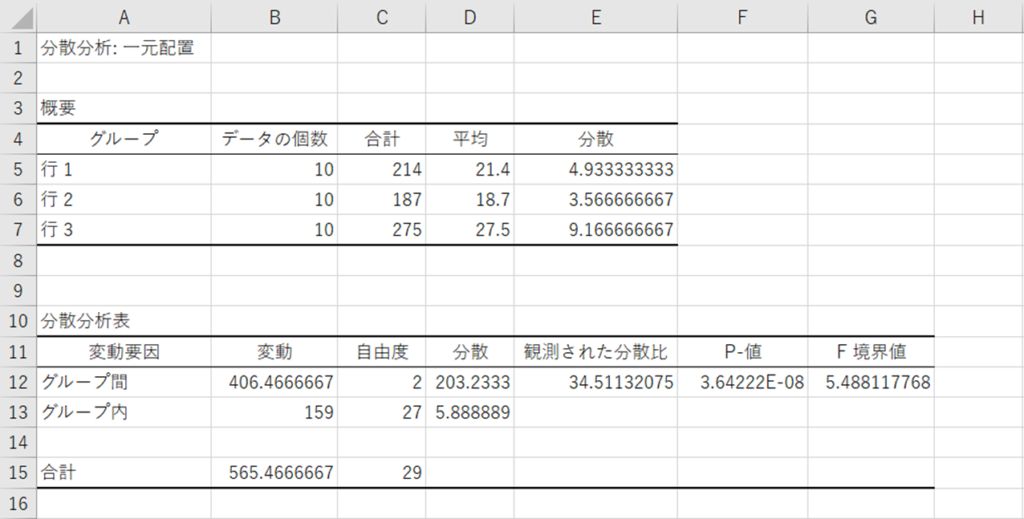
OKを押すと出力は
検定における仮説
検定統計量\(F_0\)は
帰無仮説\(H_0 \): 肥料の水準により違いは生じない
自由度\(Φ_A , Φ_E\)のF分府に従う
統計検定量から算出されたP値が
上記の分散分析表を見ると
P値は\(3.64222E-08\)より
この値は、0.0000000364と同じです。
通常、P値が0.05以下であれば、
統計的に有意と見なされますが、
P値が非常に小さい場合、
より強い統計的な有意性が示されます。
したがって、P値が3.64×10のマイナス8乗であれば、
帰無仮説は棄却され
肥料の違いにより
収穫量の差があると言える


