あい
今回はエクセルで
Q-Qプロット
(キュムプロット)を
実装します
[PR]※本サイトにはプロモーションが含まれています
合わせて読みたい
目次
Q-Qプロット(Quantile-Quantile Plot)
Q-Qプロットは
データの分布が正規分布かどうか判断する。
そしてデータの分布が確認できる
グラフです。
横軸が値、縦軸が累積確率を示します。
また異常値の検出にもQ-Qプロットが利用されます。

あい
度数分布表から
キュムプロットを
作る方法を教えちゃいます
累積ヒストグラム(Cumulative Histogram)
- 度数表から相対度数を求める。
- 各区間が昇順になっているか確認し累積度数を求める。
- 横軸に区間名縦軸に累積相対度数(確率)をとり
累積度数(確率)をプロットする。
度数表から相対度数を求める

あい
データ範囲は1~100
区間は10
度数は区間に
入る数です

- 区間1(0以上10未満のデータ)…..2
- 区間2(10以上20未満のデータ)….4
- 区間3(20以上30未満のデータ)….6
- etc・・

あい
次に各区間の度数を
データサイズで割った
相対度数を求めて
いきます
各区間1からnまでの度数を\({x_1,x_2,x_3….x_n}\)とすると
区間nの相対度数 \(=\displaystyle\frac{x_n}{データサイズ}\)
で相対度数を求めます

あい
上記の度数表をから
相対度数を計算します!
今回は小数点第二位に丸めます!


あい
各区間が
昇順になっているか
確認します
区間はちゃんと
昇順になってますね
各区間が昇順になっているか確認し累積度数を求める
- 区間1の相対度数(確率)が0.04なので
区間1の累積度数(確率)を0.04にします。 - 区間の相対度数(確率)が0.08なので
区間1の累積度数(確率)を
区間2に加え0.12とします。 - この処理を区間10まで上記を繰り返します!

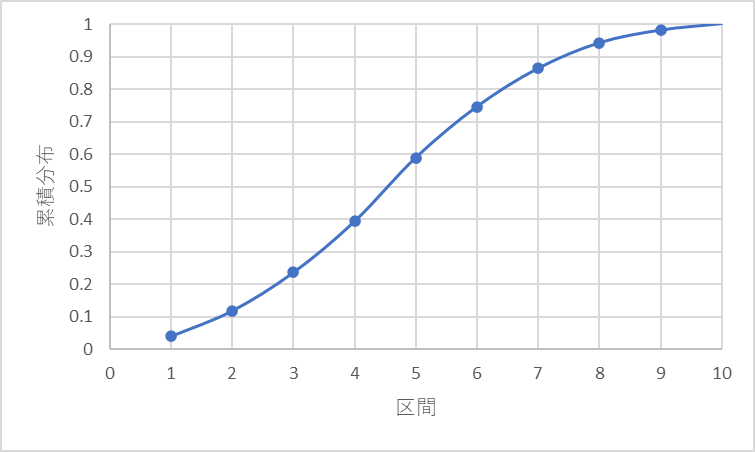
横軸に区間名、縦軸に累積相対度数(確率)をとりプロットする

あい
データから
Q-Qプロットを
作ります

あい
縦軸は区間
縦軸は累積分布
になってますね
Q-Q Plotを作ろう
- データを昇順に並び替える。
- 各データの累積度数(確率)を求める
- 横軸に観測値縦軸に累積度数(確率)で
各データの累積度数(確率)をプロットする
データを昇順に並び替える

あい
データを
昇順に並び替えます
昇順に並べた51個のデータ
5.2,9.1,12.1,15.2,16.6,18,22,23,26.2,26.6,28.2,28.9,32.3,34.1,35,36,36.2,38,39.2,39.7,41,41.4,42.1,43.1,45,46,47,47.7,48.4,49,51,52.2,53,53.5,54.2,55.2,57.1,58,62,63,65,66.1,68,69.2,71,72.2,73,77,82.1,88.8,91.2
5.2,9.1,12.1,15.2,16.6,18,22,23,26.2,26.6,28.2,28.9,32.3,34.1,35,36,36.2,38,39.2,39.7,41,41.4,42.1,43.1,45,46,47,47.7,48.4,49,51,52.2,53,53.5,54.2,55.2,57.1,58,62,63,65,66.1,68,69.2,71,72.2,73,77,82.1,88.8,91.2

あい
データ1値の
相対度数と
累積度数(確率)
を計算すると
累積度数(確率)を求める
| データ | 相対度数 | 累積度数 |
| 5.2 | 0.02(0.01961) | 0.02 |
| 9.1 | 0.02 | 0.039 |
| 12.1 | 0.02 | 0.059 |
| 15.2 | 0.02 | 0.078 |
| 16.6 | 0.02 | 0.098 |
| 最後まで続く | to be continue・・ | to be continue・・ |
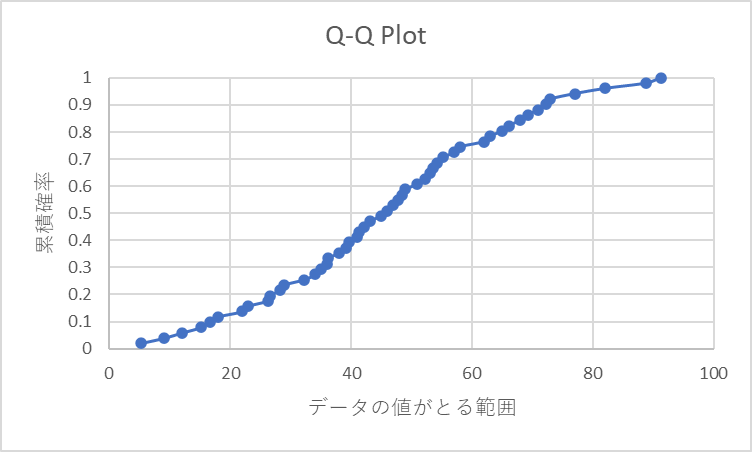
累積度数(確率)をプロットする

あい
これがキュムプロットです
正規分布とQ-Q plot

あい
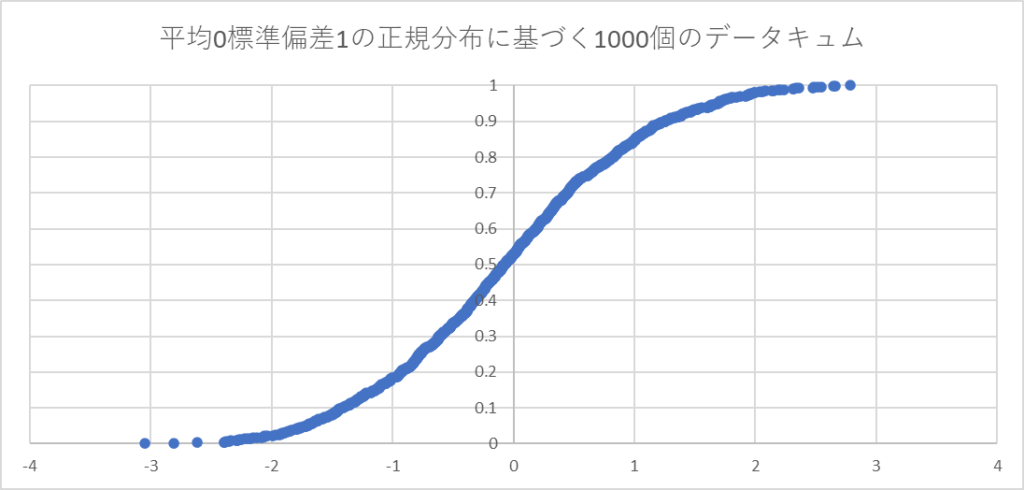
1000個の平均0標準偏差1の
正規分布に基づくデータ
からキュムプロット
を引いていきます

あい
このグラフに近いほど
正規分布に近い
ことが判断できますね
異常値の検出
データの特性や異常値の検出にも
Q-Qプロットが利用されます。
例題を使って見ていきましょう。
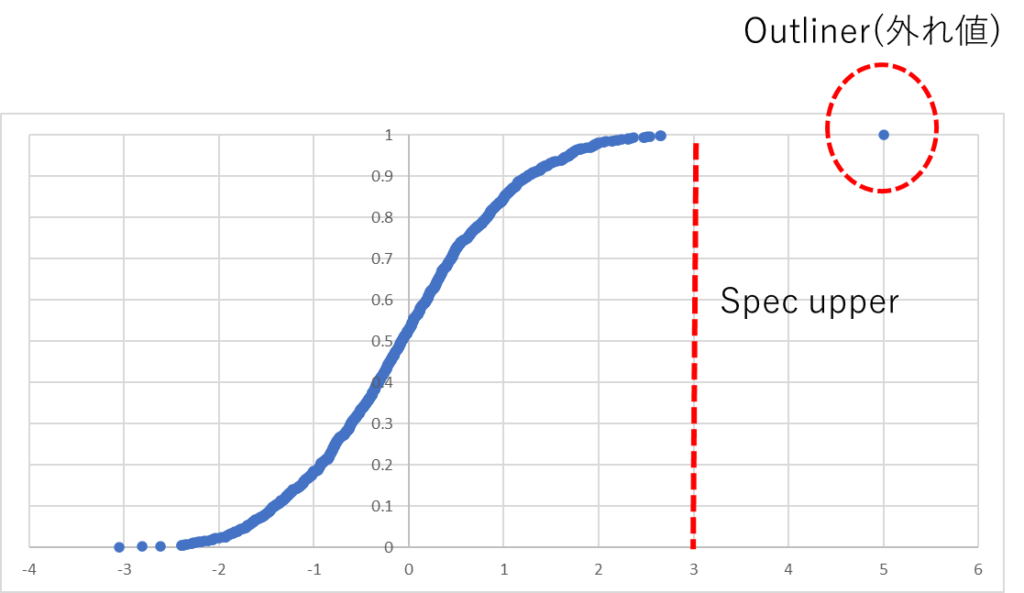
上限値=3を設定し1000個のデータの内値が3を超えていた場合不良とする
Q-Q plotを引いてデータの分布を確認し分析せよ
Outliner(外れ値)

あい
1つだけ外れ値が
あることが判断
しました
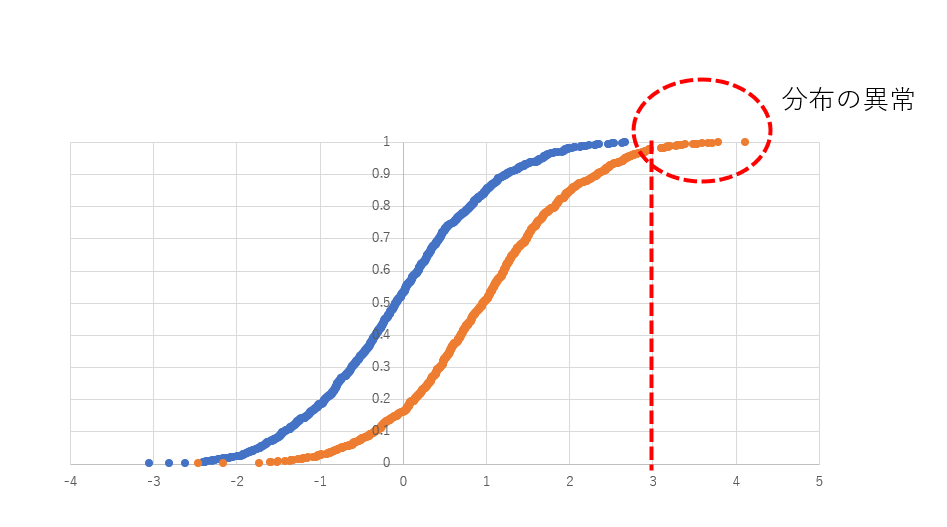
分布がスペックを外れている

あい
オレンジの
分布がおかしいですね