今回は2つの物事の
関係性を示す
相関関係
散布図
相関係数に
ついて説明します
[PR]※本サイトにはプロモーションが含まれています
| 合わせて読みたい | 記事の内容 |
| 【Python】散布図を用いたアヤメの特徴分析方法 | 有名なアヤメのデータセットをpythonを利用し 散布図を作成、アヤメの種類の特徴量をデータで示しています |
| groupbyメソッドを利用して層別散布図を作る | groupbyメソッドを利用して層別散布図を作成してみました |
| 散布図行列(Scatter plot matrix)と相関行列(Correlation matrix)をpythonで実装する | 散布図行列と相関行列について説明しpythonで実装しています |
目次
相関関係とは?
1つの変数が変化すると
それに対応してもう1つの変数も変化する関係のこと
例えば
勉強を頑張った分だけ
テストの点数がよくなった
データがあります。
我々はそれを見て
勉強時間が変化すれば
テストの点数も変化すると考えます
つまり勉強時間とテストの点数は
相関関係があると
いうことです
散布図(Scatter Plot)とは?
散布図(Scatter Plot)は
2つの連続的な変数(数値データ)の関係を
視覚的に表現するためのデータ可視化手法です。
横軸に1つの変数、縦軸にもう1つの変数を配置し
データポイントを点としてプロットすることで
変数間の相互関係やパターンを直感的に理解しやすくします。

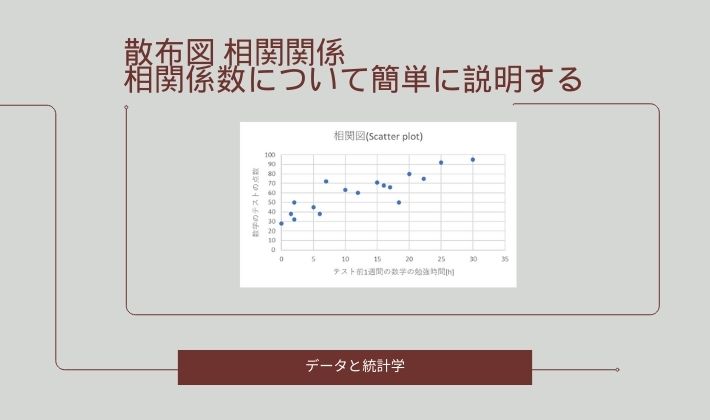
下に散布図を描きます!
横軸はテスト1週間前の
数学の勉強時間
縦軸は数学の
テストの点数を配置し
散布図を作成しています

散布図を見ると
テストを頑張った
人ほど点数が
良くなってる
ように見えるね!
散布図を見るポイント
- 異常値がないかどうか調べる
- 層別の必要がないか調べる
- 調べる前に相関がありそうな2変数にあたりをつけておく
散布図の種類
正の線形相関(Positive Linear correlation)
2つの変数が直線的に関連しています
一方の変数が増加すると
他方の変数も増加する傾向があり
データは右上がりの傾向を持ちます。
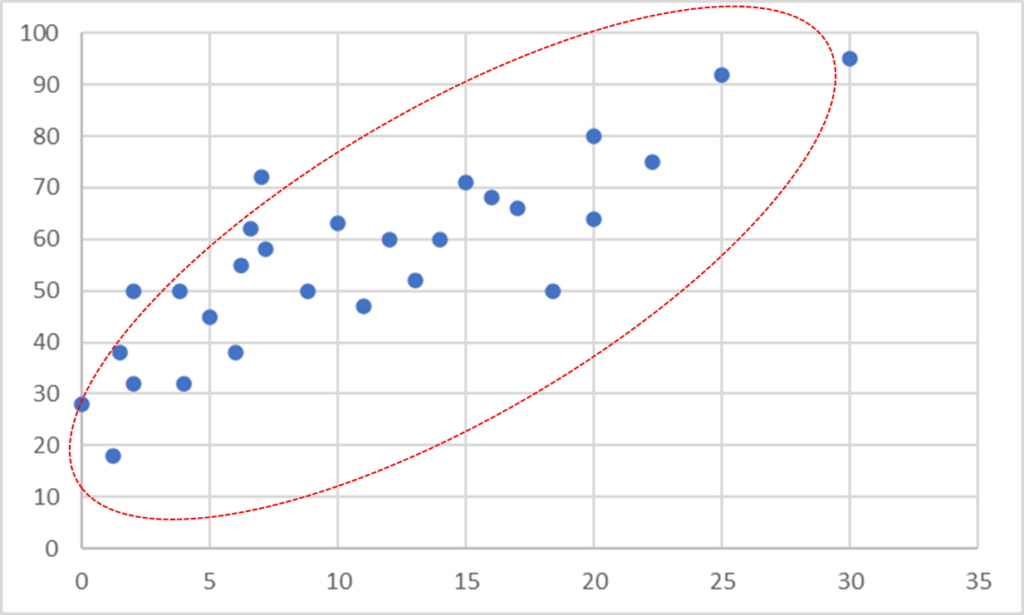

1つの変数が
大きいともう一つの
変数も大きい
右肩上がり♪
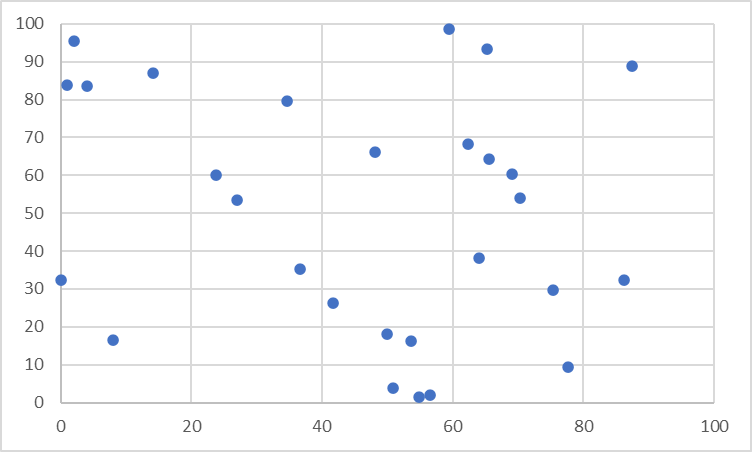
無相関(No Correlation)
2つの変数が互いに影響を与えない
散布図を見てみると規則性はありません。
負の線形相関(Negative Linear Correlation)
2つの変数が直線的に関連しています
一方の変数が増加すると
他方の変数も減少する傾向があり
データは右下がりの傾向を持ちます。
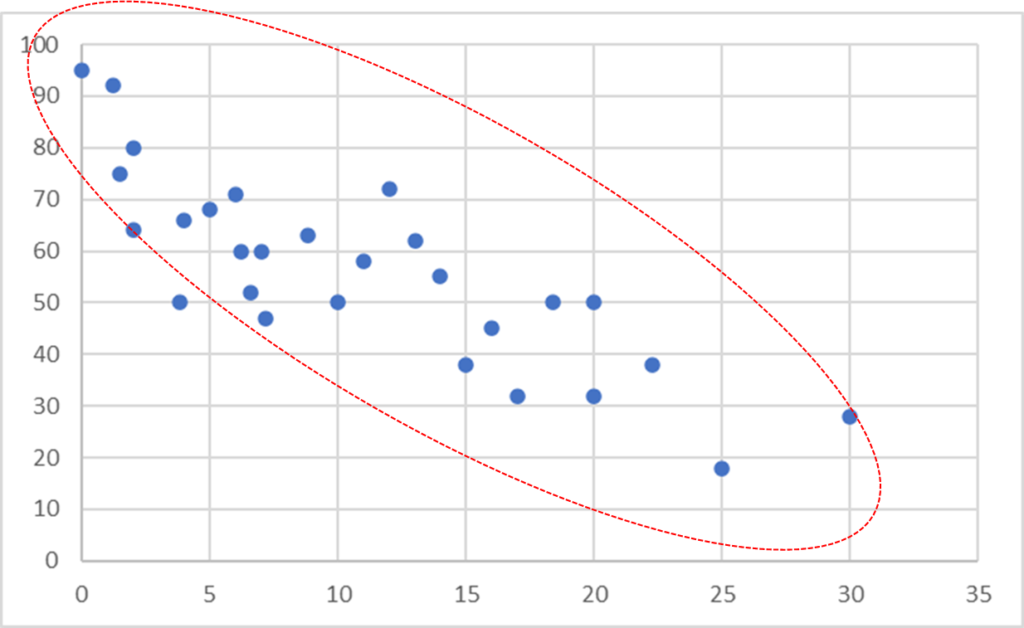

1つの変数が
大きいともう一つの
変数は小さい
右肩下がり。。。
非線形相関(Non-Linear Correlation)
非線形相関は、変数間の関係が直線的ではなく
曲線的な傾向があり
散布図上でデータポイントは
曲線や非直線的な傾向を持ちます。


ぐにゃっとしてる~
相関係数(Correlation Coefficient)
相関係数はピアソンの相関係数として
知られており
2つの変数の間の相関関係を数値化
した指標です。
相関係数は変数間の直線の関係を評価します。
相関係数の式を紹介します
\(\displaystyle r= \frac{S_{xy}}{\sqrt{S_xS_y}}\)
平方和が式に利用されています!
上記の式を更に分解すると
\(\displaystyle r=\frac{\sum_{k=1}^{n}{(x_k-\overline x)(y_k-\overline y)}}{\sqrt{\sum_{k=1}^{n}{(x_k-\overline x)^2}\sum_{k=1}^{n}{(y_k-\overline y)^2}}}\)

式長…
相関係数の見方を教えます
以上の式から算出した値は-1から1までの間を取ります。
- 1に近い場合: 強い正の相関がある。
>一方の変数が増加すると他方の変数も増加する傾向がある。 - -1に近い場合: 強い負の相関がある。
>一方の変数が増加すると他方の変数は減少する傾向がある。 - 0に近い場合: 相関が弱いかない
変数間にはほとんど相関がない

散布図は視覚的
相関係数は数値的に
相関関係を
確認することが
できるのか ~
偏相関係数(Partial Correlation Coefficient)
偏相関係数は
3つ以上の変数間の相関を評価するための指標です。
偏相関係数は、特定の2つの変数の間の相関を評価する際に
他の変数の影響を
制御するために使用されます。
言い換えれば
偏相関係数は、
他の変数の影響を除去して
2つの変数の直接の相関を
評価するための手法です。
| 3変数 | 相関係数 | 相関関係 |
| 部屋の大きさと家賃 | 0.8 | 強い正の相関 |
| 部屋の大きさと築年数 | 0.5 | やや強い正の相関 |
| 家賃と築年数 | 0.2 | 弱い正の相関 |
相関係数から論理を纏めると…
- 家賃が大きいほど家賃が高くなる
- 部屋の大きさと築年数には相関関係がある
- 家賃が高いほど築年数(古い物件が多い) ?

古いおうちほど
安いんじゃないの…?
三変数の相関関係を表にすると

ピアソンの相関係数に代わり
偏相関係数を利用して
家賃と築年数の相関関係を確認していきます
偏相関係数の公式は…
\(\displaystyle r_{xy・z}=\frac{r_{yz}-r_{xy}r_{xz}}{\sqrt{1-r_{xy}^2}\sqrt{1-r_{xz}^2}}\)
(x,y,z)=(大きさ、家賃、築年数)とすると
\(r_{xy}=0.8,r_{xz}=0.5,r_{yz}=0.2\)
\(r_{xy・z}=-0.288\)
弱い負の相関になったので家賃が安いほど
建物が古い傾向であることが分かる。
相関分析の時の注意点
- 相関関係と因果関係は異なる
- 因果関係がなくても2変数の相関関係が大きくなる可能性がある。
- 2つの変数に第3の変数の値が大きく影響している可能性がある。
これを見かけ上の相関(擬相関)という