
今回は一元配置法を利用して
分散分析を説明します
[PR]※本サイトには、プロモーションが含まれています
目次
分散分析(ANOVA: Analysis of Variance)とは?
分散分析とは
ばらつきを分けて解析する方法です
具体的にいうと
ある因子の影響によって
発生するばらつきが
統計的に有意かどうかを評価する手法です
次に分散分析の手順を示します。
分散分析(一元配置法)の手順
ある農場で
3つの異なる肥料の効果を比較するために
同じ作物を用いて実験が行われました
各肥料をランダムに選んで
それぞれ10区画に適用しました。
収穫量(kg)を見て
肥料の効果を比較するために
分散分析を実施します。
| 水準 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 合計 | 平均 |
| 肥料A | 18 | 20 | 22 | 25 | 24 | 21 | 19 | 23 | 20 | 22 | 214 | 21.4 |
| 肥料B | 17 | 16 | 18 | 19 | 20 | 21 | 22 | 19 | 18 | 17 | 187 | 18.7 |
| 肥料C | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 275 | 27.5 |
データをプロットします
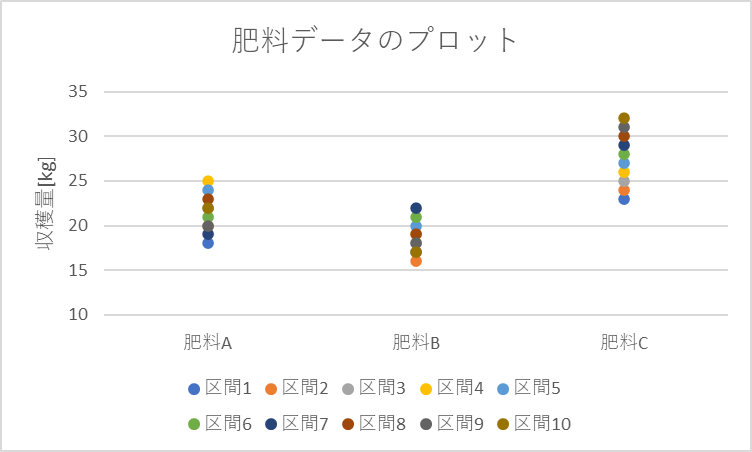

肥料の違いで差があり
肥料Cを利用した時の収穫量
が一番良いように見えますね!
肥料の違いによって
収穫量に差があるのか
統計学を利用して
判断する手法として
分散分析を紹介します
データの分解
肥料の変更以外で発生するばらつきを実験誤差
肥料の種類によって発生するばらつき
と2つに区分して考えていく
肥料の種類によって発生するばらつきが
肥料の変更以外で発生するばらつきに比べて
大きければ肥料による違いを認めることが出来る
同じぐらいであれば肥料による違いは
誤差程度であると考える

データを\(x_{ij}\)と置いてデータを分解してみる
iを肥料の種類
jを繰り返し番号
データを次のように分解します
\(x_{ij}-\bar {\bar x}=(\bar x_{i・} – \bar{\bar x})+(x_{ij} – \bar x_{i・})\)
\(x_{ij}- \bar{\bar x}\)は個々のデータと全平均の差
\(\bar x_{i・} – \bar{\bar x}\)は肥料ごとの平均と全平均の差
\(x_{ij} – \bar x_{i・}\)は個々のデータと肥料ごとの平均の差
\(個々のデータと全平均の差\)
\(=肥料ごとの平均と全平均の差+個々のデータと肥料ごとの平均の差\)
実際のデータを分解していきます。
全平均\(\bar { \bar x}=22.53 ≒ 22.5\)
\(x_{ij}-\bar {\bar x}\)
| -4.5 | -2.5 | -0.5 | 2.5 | 1.5 | -1.5 | -3.5 | 0.5 | -2.5 | -0.5 |
| -5.5 | -6.5 | -4.5 | -3.5 | -2.5 | -1.5 | -0.5 | -3.5 | -4.5 | -5.5 |
| 0.5 | 1.5 | 2.5 | 3.5 | 4.5 | 5.5 | 6.5 | 7.5 | 8.5 | 9.5 |
\(\bar x_{i・} – \bar{\bar x}\)
| -1.1 | -1.1 | -1.1 | -1.1 | -1.1 | -1.1 | -1.1 | -1.1 | -1.1 | -1.1 |
| -3.8 | -3.8 | -3.8 | -3.8 | -3.8 | -3.8 | -3.8 | -3.8 | -3.8 | -3.8 |
| 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
\(x_{ij} – \bar x_{i・}\)
| -3.4 | -1.4 | 0.6 | 3.6 | 2.6 | -0.4 | -2.4 | 1.6 | -1.4 | 0.6 |
| -1.7 | -2.7 | -0.7 | 0.3 | 1.3 | 2.3 | 3.3 | 0.3 | -0.7 | -1.7 |
| -4.5 | -3.5 | -2.5 | -1.5 | -0.5 | 0.5 | 1.5 | 2.5 | 3.5 | 4.5 |
ばらつきの評価を行うためそれぞれを2乗する
\((x_{ij}-\bar {\bar x})^2\)
| 20.25 | 6.25 | 0.25 | 6.25 | 2.25 | 2.25 | 12.25 | 0.25 | 6.25 | 0.25 |
| 30.25 | 42.25 | 20.25 | 12.26 | 6.25 | 2.25 | 0.25 | 12.25 | 20.25 | 30.25 |
| 0.25 | 2.25 | 6.25 | 12.25 | 20.25 | 30.25 | 42.25 | 56.25 | 72.25 | 90.25 |
個々のデータと全体平均の差を
二乗した総和を総平方和といい以下の式から求める
\(\displaystyle S_T =\sum_{i=1}^{3}\sum_{j=1}^{10} (x_{ij}-\bar {\bar x})^2=565.5\)
\((\bar x_{i・} – \bar{\bar x})^2\)
| 1.21 | 1.21 | 1.21 | 1.21 | 1.21 | 1.21 | 1.21 | 1.21 | 1.21 | 1.21 |
| 14.44 | 14.44 | 14.44 | 14.44 | 14.44 | 14.44 | 14.44 | 14.44 | 14.44 | 14.44 |
| 25 | 25 | 25 | 25 | 25 | 25 | 25 | 25 | 25 | 25 |
肥料ごとの平均と全平均の差を
二乗したものの総和をA間平方和といい以下の式から求める
\(\displaystyle S_A =\sum_{i=1}^{3}\sum_{j=1}^{10}(\bar x_{i・} – \bar{\bar x})^2 =406.5\)
\(x_{ij} – \bar x_{i・}\)
| 11.56 | 1.96 | 0.36 | 12.96 | 6.76 | 0.16 | 5.76 | 2.56 | 1.96 | 0.36 |
| 2.89 | 7.29 | 0.49 | 0.09 | 1.69 | 5.29 | 10.89 | 0.09 | 0.49 | 2.89 |
| 20.25 | 12.25 | 6.25 | 2.25 | 0.25 | 0.25 | 2.25 | 6.25 | 12.25 | 20.25 |
個々のデータと肥料ごとの平均の差を
二乗したものの総和を誤差間平方和
といい以下の式から求める
\(\displaystyle S_E =\sum_{i=1}^{3}\sum_{j=1}^{10} (x_{ij} – \bar x_{i・})^2=159\)
平方和
各データの平方和に関して以下の関係が成り立つ
\(S_T = S_A + S_E \)
\(\displaystyle S_T =\sum_{i=1}^{3}\sum_{j=1}^{10} (x_{ij}-\bar {\bar x})^2=565.5\)
\(\displaystyle S_A =\sum_{i=1}^{3}\sum_{j=1}^{10}(\bar x_{i・} – \bar{\bar x})^2 =406.5\)
\(\displaystyle S_E =\sum_{i=1}^{3}\sum_{j=1}^{10} (x_{ij} – \bar x_{i・})^2=159\)
\(S_A\)をそれぞれの肥料によるばらつき
\(S_E\)をそれぞれの誤差によるばらつき
と考える分散分析はばらつきを評価する
手法だが平方和のまま比較はできない
平方和から分散を求めて比較する必要がある
分散
分散は平方和を自由度で割る
\(\displaystyle V_A = \frac{S_A}{Φ_A}\)
\(\displaystyle V_E = \frac{S_E}{Φ_E}\)
自由度
肥料の違いは3種類
\(\bar x_{1・} – \bar{\bar x}=-1.13≒-1.1\)
\(\bar x_{2・} – \bar{\bar x}=-3.83≒-3.8\)
\(\bar x_{3・} – \bar{\bar x}=4.97≒5.0\)
計算結果より3種のデータの総和は≒0
つまり2つの値が決まればよい
\(S_A\)は2つの情報で構成されるので
\(Φ_A= 2\)
\(V_A=406.5/2=203.25\)
\(S_E\)も30個データがあるが
平方する前のデータを見てみると
最後の行は9行決まれば10行目の値が決まる
\(Φ_E= 30- 3=27\)
\(V_E= 159/27=5.89\)
次に\(V_AとV_E\)を比較するための
検定統計量を求める
\(\displaystyle F_0 =\frac{V_A}{V_E} \)
\(\displaystyle F_0 =\frac{V_A}{V_E} = 34.51 \)
分散分析表
| 要因 | 平方和 | 自由度 | 分散 | \(F_0\) |
| A | 406.5 | 2 | 203.25 | 34.51 |
| E | 159 | 27 | 5.89 |
分散分析による仮説検定
目的は肥料によって収穫量に違いがあることを
上記を踏まえた上で帰無仮説、対立仮説
を設定する
帰無仮説は\(H_0\) : 肥料による違いはない
対立仮説は\(H_1\) : 肥料による違いがある
\(H_0 : μ_1 = μ_2 = μ_3\)
\(H_1 : H_0が成り立たない\)
検定統計量\(F_0\)は
帰無仮説\(H_0 \)の元で
自由度\(Φ_A , Φ_E\)のF分府に従う
片側検定の棄却域を設定する
\(R : F_0 ≧F(Φ_A ,Φ_E , α)\)
\(R : F_0 ≧F(2 ,27 , 0.01)=5.49\)
分散分析表を見ると
\(F_0 = 34.51\)より
統計的に有意である以上より
帰無仮説は棄却され
肥料の違いにより
収穫量の差があると判断する
最適な肥料による収穫量の推定と予測
次にどの肥料によって
収穫量が多くなるか最適水準の
推定をしてみる
点推定 : \(\hat μ_i = \bar x_{i・}\)
区間推定 : 信頼率100(1-α)%の信頼区間
\((\displaystyle \hat x_i・-t(Φ_E , α)\sqrt{\frac{V_E}{r}} ,\) \hat x_i・+t(Φ_E , α)\sqrt{\frac{V_E}{r}})\)
点推定は各肥料の収穫量の平均なので
| 水準 | 収穫量(Kg)の平均 |
| 肥料A | 21.4 |
| 肥料B | 18.7 |
| 肥料C | 27.5 |
収穫量の推定量は
肥料Cを利用した時が一番大きいので
肥料Cが最適水準と考える
肥料Cを利用した時
収穫量95%の信頼区間は
\((\displaystyle 27.5・-t(27 , 0.05)\sqrt{\frac{5.89}{2}} , \hat x_i・+t(27 , 0.05)\sqrt{\frac{5.89}{2}})\)
\([23.97,31.02]\)
もう一度同じ実験を行った時の
予測値は以下のようになる
点予測 : \(\hat μ_i = \bar x_{i・}\)
区間予測 : 信頼率100(1-α)%の予測区間
\((\displaystyle \hat x_i・-t(Φ_E , α)\sqrt{(\frac{1}{r}+1)V_E} , \)
\(\hat x_i・+t(Φ_E , α)\sqrt{(\frac{1}{r}+1)V_E})\)
分散分析基本用語
| 用語 | 意味 |
| 因子 | 特性値,このページでは肥料の事 |
| 水準 | 因子の条件を変更した段階,このページでは肥料は3種類 つまり3水準 |
| 自由度 | 平方和を割る定数 |
| 平均平方 | 分散のこと |
| 主効果 | 因子による特性値の影響度 |
| 交互作用効果 | 2つの因子による組み合わせによる特性値の影響度 |
| 要因 | 主効果,交互作用効果,繰り返しの総称 |
| 繰り返し | 実験及び測定の繰り返し |
参考文献


第6章 分散分析より


