
今回はロジスティック回帰
モデルについて
糖尿病の疾患確率と
血糖値のデータを使って
モデル化し説明します
[PR]※本サイトにはプロモーションが含まれています
今回使うデータセット
Pima Indian Diabetesデータセット
– 糖尿病の発症を予測するためのデータセット
| データセットの項目説明 | 特徴 |
| Pregnancies | 妊娠回数(回) |
| Glucose | 血糖値(mmg/dl) |
| BloodPressure | 血圧(mmHg) |
| SkinThickness | 皮膚の厚さ(mm) |
| Insulin | 血中インスリン値(μU/mL) |
| BMI | 身長と体重から計算された値(kg/m²) |
| DiabetesPedigreeFunction | 糖尿病の家族関係 |
| Age | 患者の年齢 |
| Outcome | 糖尿病の有無(0 : 無,1有) |
以下コードで取得してください
import pandas as pd
# データセットのURL
url = "https://raw.githubusercontent.com/jbrownlee/Datasets/master/pima-indians-diabetes.data.csv"
# カラム名を指定
column_names = [
"Pregnancies", "Glucose", "BloodPressure", "SkinThickness",
"Insulin", "BMI", "DiabetesPedigreeFunction", "Age", "Outcome"
]
# データを読み込む
data = pd.read_csv(url, header=None, names=column_names)
print(data.head(5))実行結果
Pregnancies Glucose BloodPressure SkinThickness Insulin BMI DiabetesPedigreeFunction Age Outcome
0 6 148 72 35 0 33.6 0.627 50 1
1 1 85 66 29 0 26.6 0.351 31 0
2 8 183 64 0 0 23.3 0.672 32 1
3 1 89 66 23 94 28.1 0.167 21 0
4 0 137 40 35 168 43.1 2.288 33 1ロジスティック回帰モデルとは ?
予測したいデータ(目的変数)が
0か1(発生確率)の際
使用される統計モデルです
具体的な事例で説明します
糖尿病の有無をデータから予測したいと考えています
糖尿病は血液中のグルコース(血糖値)と
密接に関係していると考えられています
説明変数をグルコース
目的変数を糖尿病の有無(0:無, 1:有)
とし散布図を作成します
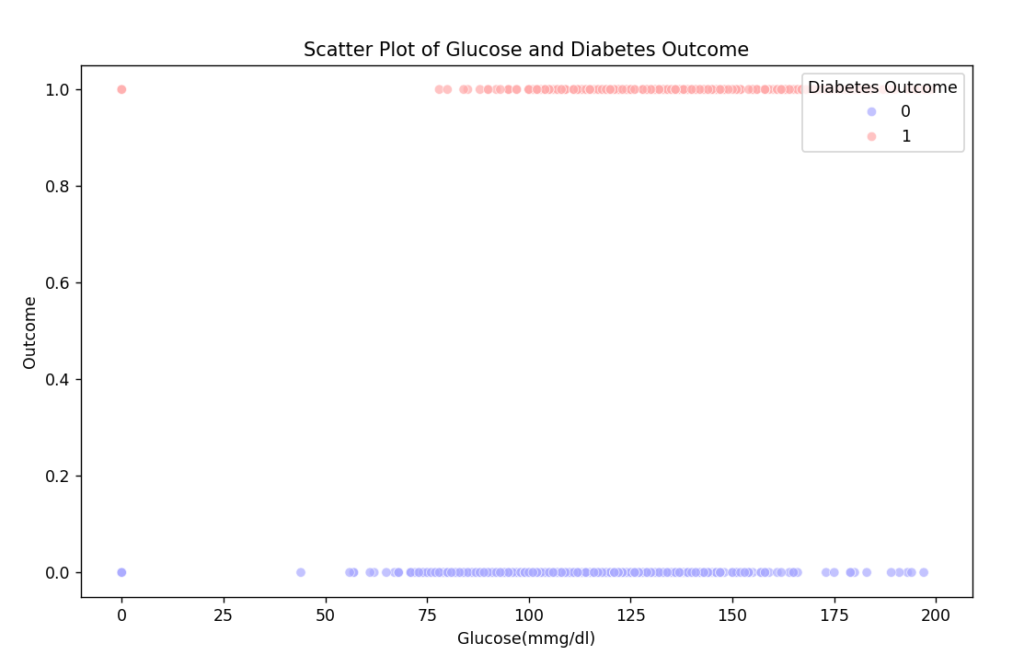
データ取得と散布図は
下記コードで実装しました
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
# データセットのURL
url = "https://raw.githubusercontent.com/jbrownlee/Datasets/master/pima-indians-diabetes.data.csv"
# カラム名を指定
column_names = [
"Pregnancies", "Glucose", "BloodPressure", "SkinThickness",
"Insulin", "BMI", "DiabetesPedigreeFunction", "Age", "Outcome"
]
# データを読み込む
data = pd.read_csv(url, header=None, names=column_names)
print(data.head(5))
# 散布図を描画
plt.figure(figsize=(10, 6))
sns.scatterplot(x='Glucose', y='Outcome', data=data, hue='Outcome', palette='bwr', alpha=0.7)
plt.xlabel('Glucose(mmg/dl)')
plt.ylabel('Outcome')
plt.title('Scatter Plot of Glucose and Diabetes Outcome')
plt.legend(title='Diabetes Outcome', loc='upper right')
plt.show() この散布図に回帰直線を採用すると
当てはまりが悪い
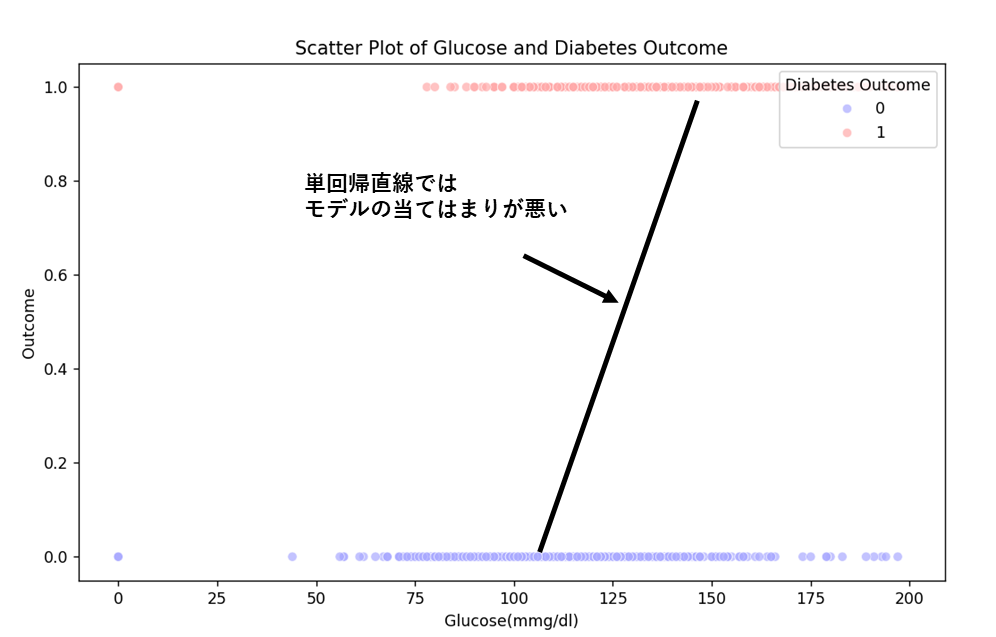
曲線モデルの方が当てはまりが良いです
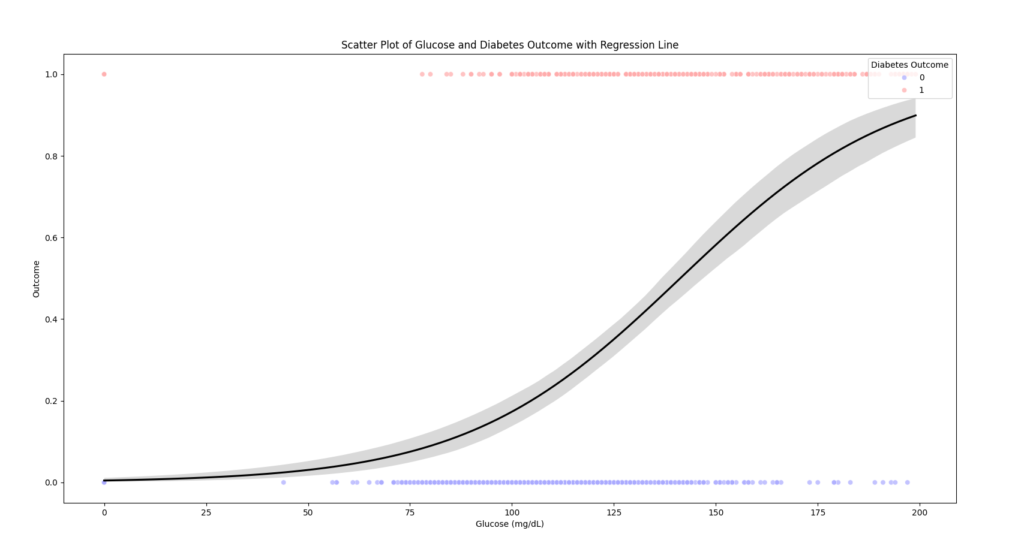
この曲線モデルを
ロジスティック回帰モデルといいます
ロジスティック関数
ロジスティック回帰モデルは
ロジスティック関数に基づいています
\(\displaystyle f(x) = \frac{exp(x)}{1 + exp(x)}\)
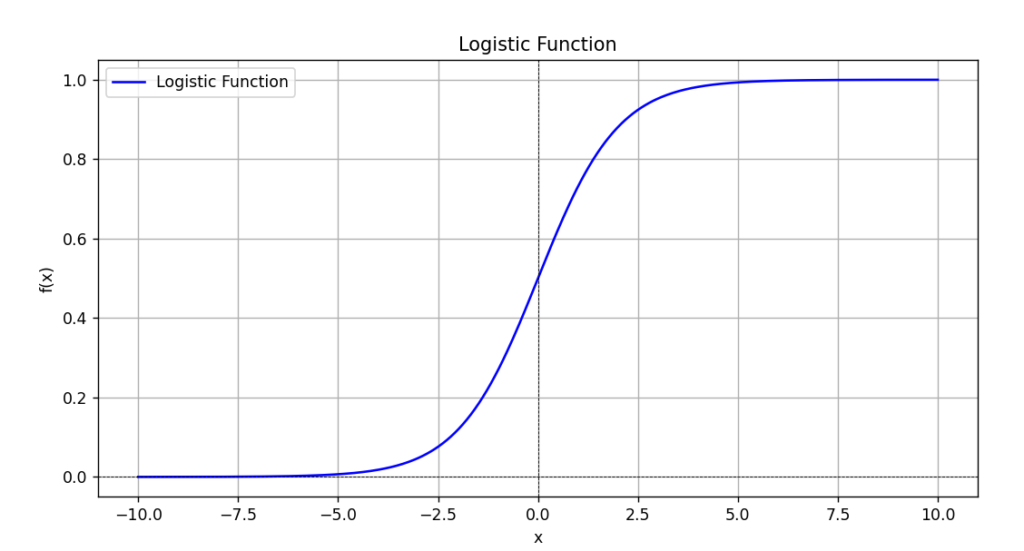
ロジスティック関数は
説明変数の区間(-∞, ∞)の値を
区間(0, 1)にうつす関数です
言い換えると
xの値を大きくしていくと
f(x)の値が1に近づく
xの値を小さくしていくと
f(x)の値が0に近づく性質があります
血液中の血糖値が高いと糖尿病(1)
血液中の血糖値が低いと糖尿病ではない(0)
といった関係性がある場合
この関数をモデルとして当てはめることができます
ロジスティック回帰モデル
血糖値を説明変数
糖尿病の疾患(疾患確率)を目的変数とすると
この関係を回帰モデルとして表現することができます
糖尿病の疾患確率をπと血糖値の値をXとすると
ロジスティック回帰モデルは以下の式で表現できる
\(\displaystyle π = \frac{exp(β_0 + β_1X)}{1 + exp(β_0 + β_1X)}\)
実データとこのモデルの当てはまりが良ければ
「血糖値とその人が糖尿病の疾患がある確率」
を予測できる
モデル性能と評価
機械学習のモデル構築では
「モデル学習に使用する訓練データ」と
「テストデータ」を入れて
訓練データから作ったモデルが
テストデータにどれだけ当てはまっているか
確認することで精度を追求することができます
下記コードを加えてください
# 訓練データとテストデータをランダムに分ける
x_train, x_test, y_train, y_test = train_test_split(X, Y, test_size=0.5, random_state=0)
# モデルを訓練する
model = LogisticRegression()
model.fit(x_train, y_train)
print("正答率(train): {:.3f}".format(model.score(x_train, y_train)))
print("正答率(test): {:.3f}".format(model.score(x_test, y_test)))splitのtest_size = 0.5でデータを2つに割っています
実行結果
正答率(train): 0.750
正答率(test): 0.742このモデルの訓練データとの正答率は75%なので
過学習は起きていないことが確認できます

血糖値と糖尿病の関係は
このモデルで大体75%は
説明でできるんですね
コード全体も置いときます
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, confusion_matrix, classification_report
# データセットのURL
url = "https://raw.githubusercontent.com/jbrownlee/Datasets/master/pima-indians-diabetes.data.csv"
# カラム名を指定
column_names = [
"Pregnancies", "Glucose", "BloodPressure", "SkinThickness",
"Insulin", "BMI", "DiabetesPedigreeFunction", "Age", "Outcome"
]
# データを読み込む
data = pd.read_csv(url, header=None, names=column_names)
print(data.head(5))
# 特徴量とターゲット変数を指定
X = data[["Glucose"]] # XをDataFrameにする
Y = data["Outcome"]
# 訓練データとテストデータをランダムに分ける
x_train, x_test, y_train, y_test = train_test_split(X, Y, test_size=0.5, random_state=0)
# モデルを訓練する
model = LogisticRegression()
model.fit(x_train, y_train)
print("正答率(train): {:.3f}".format(model.score(x_train, y_train)))
print("正答率(test): {:.3f}".format(model.score(x_test, y_test)))参考文献


第4章 ロジスティック回帰モデル


