【統計基礎】エクセルで学ぶ！時系列データの自己相関：コレログラムの作成手順

[PR]※本サイトには、プロモーションが含まれています

コレログラムとは?

コレログラム（correlogram）とは

“時系列データの自己相関を視覚的に表現するためのグラフ”です

コレログラムのグラフの横軸は

“通常ラグ0から始まりデータの長さの半分ほどのラグ(rag)”

縦軸は”自己相関係数”です

では自己相関,　ラグ(rag),　自己相関係数

とはなんでしょうか?

自己相関

自己相関は

“元のデータと時間をずらしたデータの相関“の事を言います

自己相関を確認するための処理はこんな感じです。

ラグ(Rag)を参照してデータをずらす

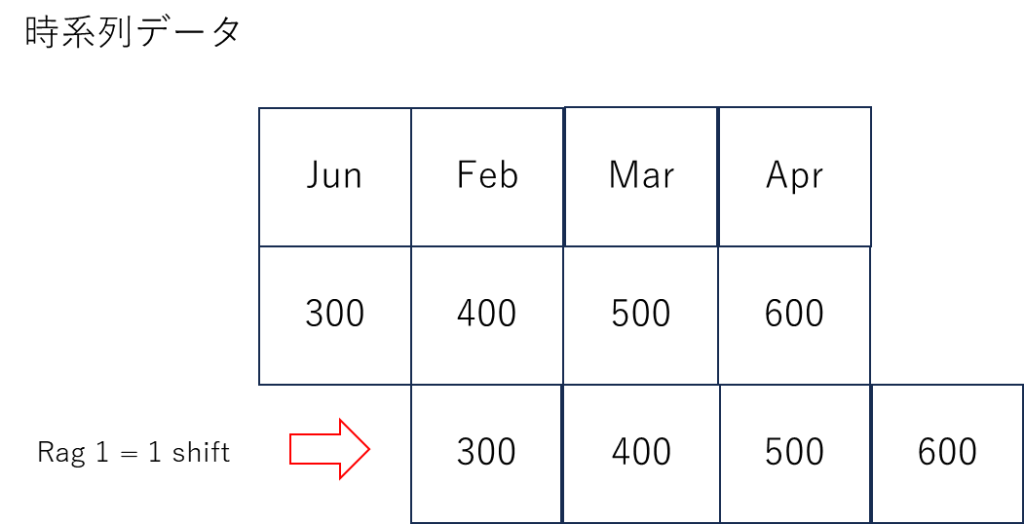
2.自己相関の大きさを測るため
元データとずらしたデータの自己相関係数を計算する

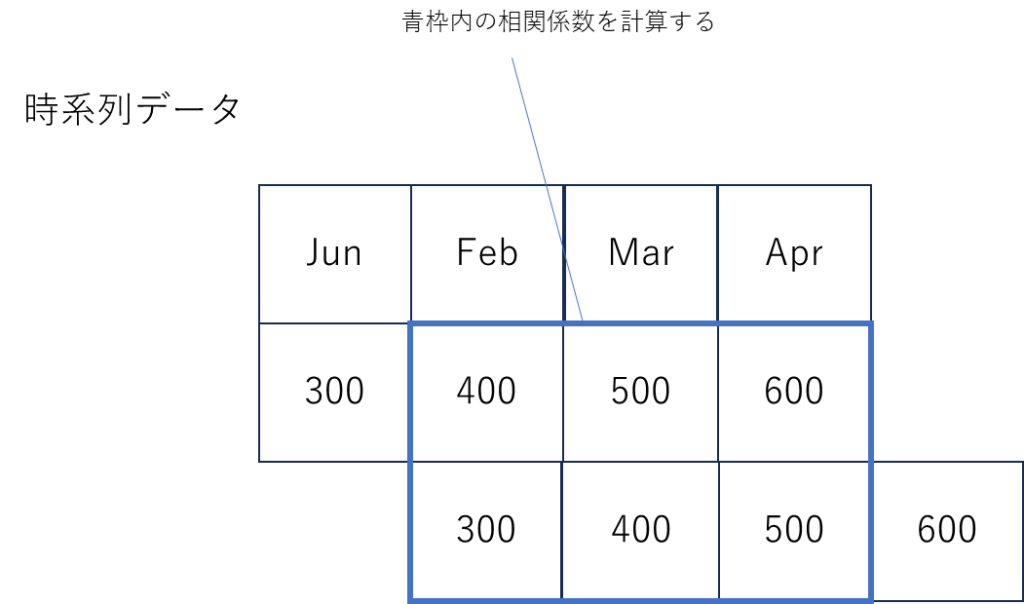
自己相関係数が0に近い場合

元データとずらしたデータの相関関係はほとんどない

自己相関関係が1に近い場合

データはほぼ一致している

自己相関関係が-1に近い場合

元データとずらしたデータは-1倍の関係に近い

ことが分かります

コレログラムの構築

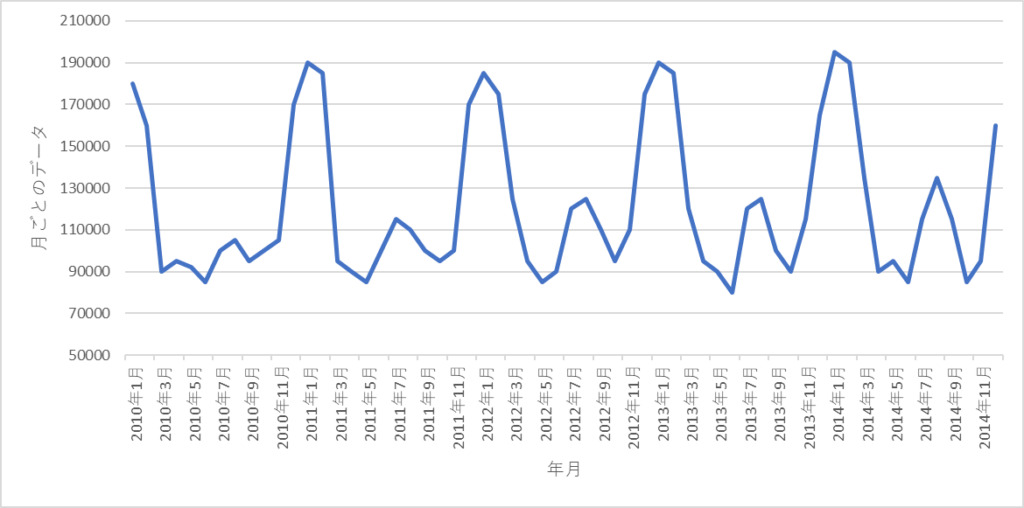
下記の時系列データから

コレログラムを作成していきます。

2010年1月から2014年12月

までの60個の仮想データを用意しました。

横軸年　月,縦軸　データ

の時系列データを作成します

コレログラムを作成するため

ラグと自己相関を計算します

ラグの作成

最初にラグを作成します

ラグ1は1つ前の時点のデータとの差を表し

ラグ2は2つ前の時点のデータとの差を表します

ラグ1はデータを1カ月後

1セル分ずらす

ラグ2はデータを2カ月後

2セル分ずらす

ラグが1つ増えるごとに

セルも1つずらしていきます

自己相関

自己相関とはラグでずらしたデータと

元データの相関関係を示す

元データ固定してxとおき

ラグデータをyにして

相関関係を確認する

ラグ0は

元データ通しの相関なので相関係数は1

ラグ1以降はエクセル関数

CORREL(データ1,データ2)を利用して

計算を行っていく

具体的な操作をして説明します

セルのC2に=CORREL($B$4:$B$63,C4:C63)

を入れ元データとrag1の相関係数を計算します

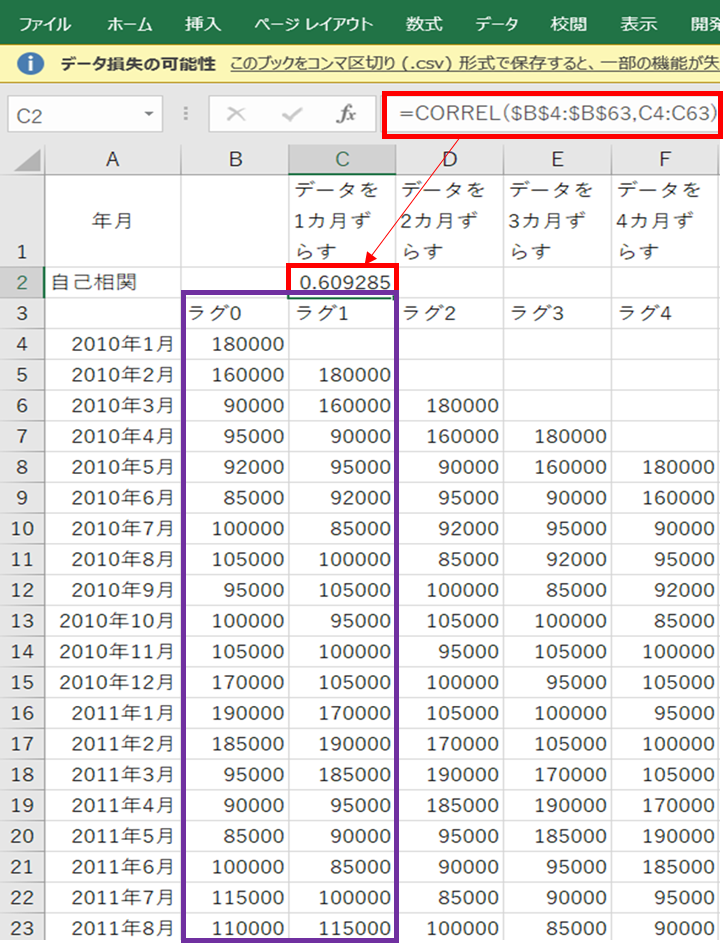
セルのC2を外側にずらして

連続データを作成する

縦軸自己相関,横軸ラグの棒グラフを作成する

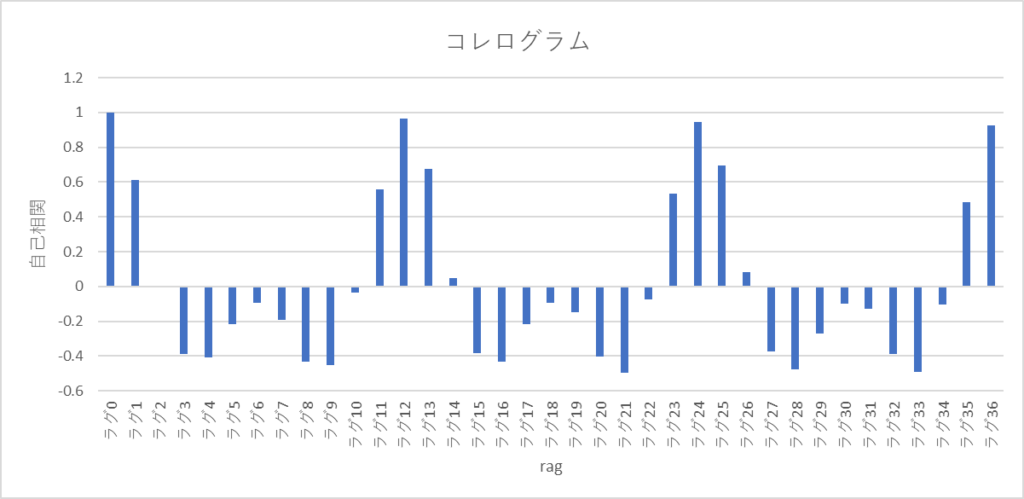
コレログラムが完成しました。

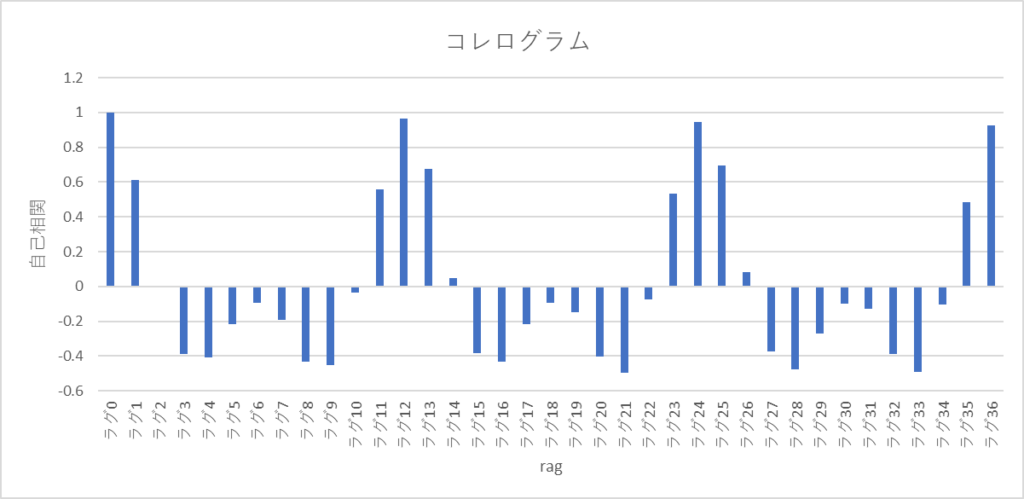
コレログラムの分析

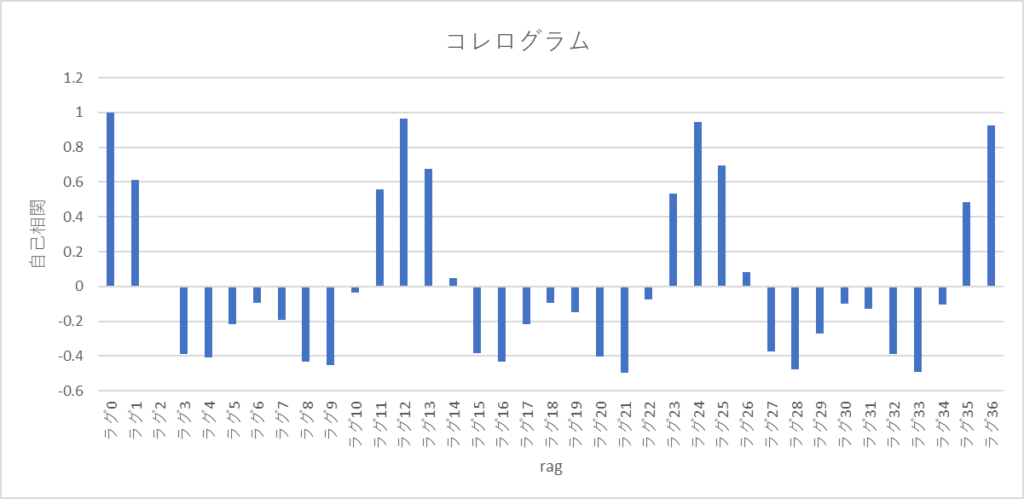
・ラグ12,24,36付近に強い正の相関がある
・ラグ3からラグ9まで負の相関がある
このデータは1年ごとに周期性を持つことが分かりますね!

参考文献