
今回はモデル選択
基準を利用して
最適な説明変数を
選択する方法を
説明します
[PR]※本サイトには、プロモーションが含まれています
目次
モデル選択基準
目的変数と説明変数との関係を表す場合
適切な説明変数を選択することが出来ないと
誤った結論を導いたり
正確なデータ予測が
出来ないといった問題が生じる
目的変数と関連している
説明変数の組み合わせを
適切に選ぶことを変数選択
説明変数を適切に選択するための基準を
モデル選択基準という

モデル選択基準を
紹介します
自由度調整済み係数
自由度調整済み係数\(R^*2\)は
決定係数を調整した基準で
以下の式で与えられます。
\(\displaystyle R^*2=max[0,1-\frac{n-1}{n-P-1}(1-R^2)]\)
nはサンプルサイズ 、pは説明変数の数
モデルに過剰な説明変数が含まれている場合
通常のR^2は高くなるが
目的変数と関連が弱い説明変数が含まれたモデル
では含まないモデルよりも値が減少する性質がある
自由度調整済みR^2はその複雑性を補正してくれます
モデル選択基準として
自由度調整済み決定係数を利用する場合
自由度調整済み決定係数の値が最も大きいモデルを
良いモデルとしてよいモデルと判断する
自由度調整済み決定係数の値が最も大きいモデルを
良いモデルとしてよいモデルと判断する
赤池情報基準AIC
最尤法で推定されたモデルを
評価するためにAICを用いる
\(AIC=-2logL(\hat β_0,…., \hat β_p, \hat σ^2)+2(p+1)\)
モデル選択基準として
赤池情報基準AICを利用する場合
AICは小さいほど良いモデルと判断する
赤池情報基準AICを利用する場合
AICは小さいほど良いモデルと判断する
ベイス型情報基準
最尤法で推定されたモデルを
評価するためにBICを用いる
\(BIC=-2logL(\hat β_0,…., \hat β_p, \hat σ^2)+(p+1)logn\)
モデル選択基準として
ベイズ型情報基準ICを利用する場合
BICは小さいほど良いモデルと判断する
ベイズ型情報基準BICを利用する場合
BICは小さいほど良いモデルと判断する

モデルを
評価する方法が
分かった!
変数選択
適切な変数を選択するには
どの説明変数の組み合わせが
最適か探して選択する必要がある
説明変数がp個の場合
組み合わせが\(p^2-1\)通りとなる
変数を選択する手法として
・総当たり法
・ステップワイズ法
が存在する
総当たり法
全ての組み合わせを総当たりで推定を行い
その都度モデル選択基準の計算を全て行い
最適なモデルを選択する手法です。
ステップワイズ法
ステップワイズ法では
変数増加法(Forward Selection)
後退選択法(Backward Elimination)がある
- 変数増加法
1つずつ変数をモデルに追加していきます
有益な変数を追加し
その変数がモデルの性能を改善するかどうかを
評価しながら進んでいきます。
説明変数を加えてもモデル選択基準の値が
改善されない場合更新を終了します - 変数減少法
全ての変数が含まれた状態から
不要と判断される変数を順次削除し
説明変数を削除してもモデル選択基準の値が
改善されない場合更新を終了します
重回帰分析
データセット
Rには、経済学のデータセットである
「Longley」が組み込まれています。
これは、アメリカの経済データを元にした
データセットであり、
7つの変数(カラム)から構成されています。longleyデータセットのカラムは以下の通りです
- GNP.deflator : GNPデフレーター
- GNP : 国民総生産
- Unemployed : 失業者数
- Armed.Force : 軍隊の人数
- Population : 人口
- Year : 年
- Employed : 雇用者数
# データの開始行を表示
head(longley)
変数選択なしで重回帰モデルを実装する
次にEmployを目的変数とした
重回帰モデルをステップワイズ法利用して
モデルを作っていきます
最初にEmploy以外の変数を
説明変数とした重回帰モデルを
Rで構築していきます。
# データの開始行を表示
head(longley)
# 雇用者数を目的変数その他の変数を目的変数とした重回帰モデルを最小二乗法で推定する
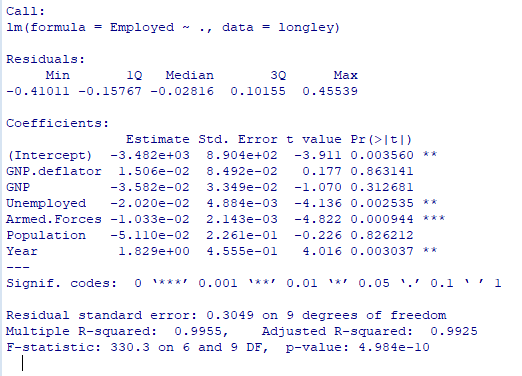
result = lm(Employed~. , data= longley)
# 推定結果の要約
summary(result)結果を見ていきます。
ステップワイズ法を利用し変数選択ありで重回帰モデルを実装する
次にstep関数を用いて変数選択を
行い新たな重回帰モデルを構築する
step関数ではモデル選択基準としてAICを用いる
# データの開始行を表示
head(longley)
# 雇用者数を目的変数その他の変数を目的変数とした重回帰モデルを最小二乗法で推定する
result = lm(Employed~. , data= longley)
# 雇用者数を目的変数その他の変数を目的変数とした重回帰モデルを最小二乗法で推定する
result = lm(Employed~. , data= longley)
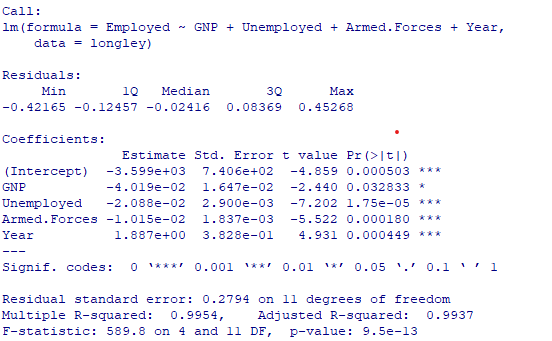
# ステップワイズ法を利用した変数選択
result.step=step(result)
# 結果の要約
summary(result.step)出力は
モデル比較
上記で作成した変数選択を行ってないモデルを
最適化前モデルとし行ったモデルを
最適化モデルと仮定しsummaryの値を
比較し評価します
評価した結果を表に纏めます

最適化後のモデルの方が良いと判断できそうです。
参考文献

(データサイエンス大系)


