今回は
単回帰モデルの
回帰係数を
最小二乗法を
利用して推定し
回帰直線を
作っていきます
[PR]※本サイトにはプロモーションが含まれています
線形単回帰モデルとは?
データから
2つの変数の関係性を
直線関係として推定
モデル化したものです
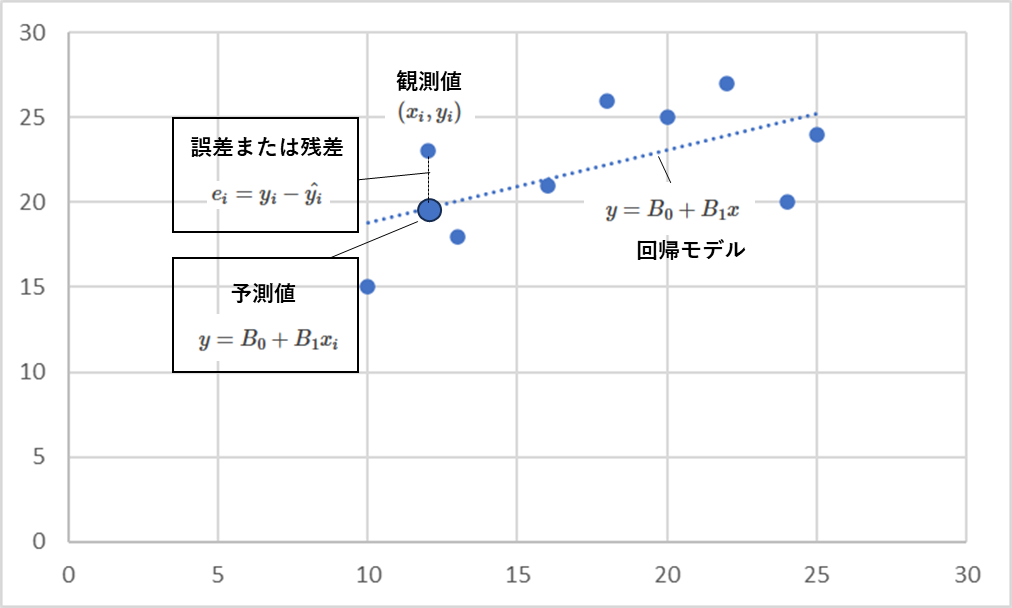
モデル化した直線を
単回帰直線といいます
2つの変数は
説明変数x(独立変数)と
目的変数yと呼ばれます
\(y=B_0+B_1x+ε\)
yは目的変数、x は説明変数
β0 は切片(y軸との交点)
β1 は回帰係数、ε は誤差

データから
直線をつくるんだ~
じゃあデータから
どうやって
直線を作るの?
回帰直線の作り方
回帰直線はデータから
作ることができます
もっと詳しい言い方をすると
最小二乗法を利用し
実データと推定された値の
誤差が最小になるように
回帰係数を計算し
回帰直線を作ります
最小二乗法とは?
データから推定される回帰直線は
実データと誤差が少ないことが
理想的です
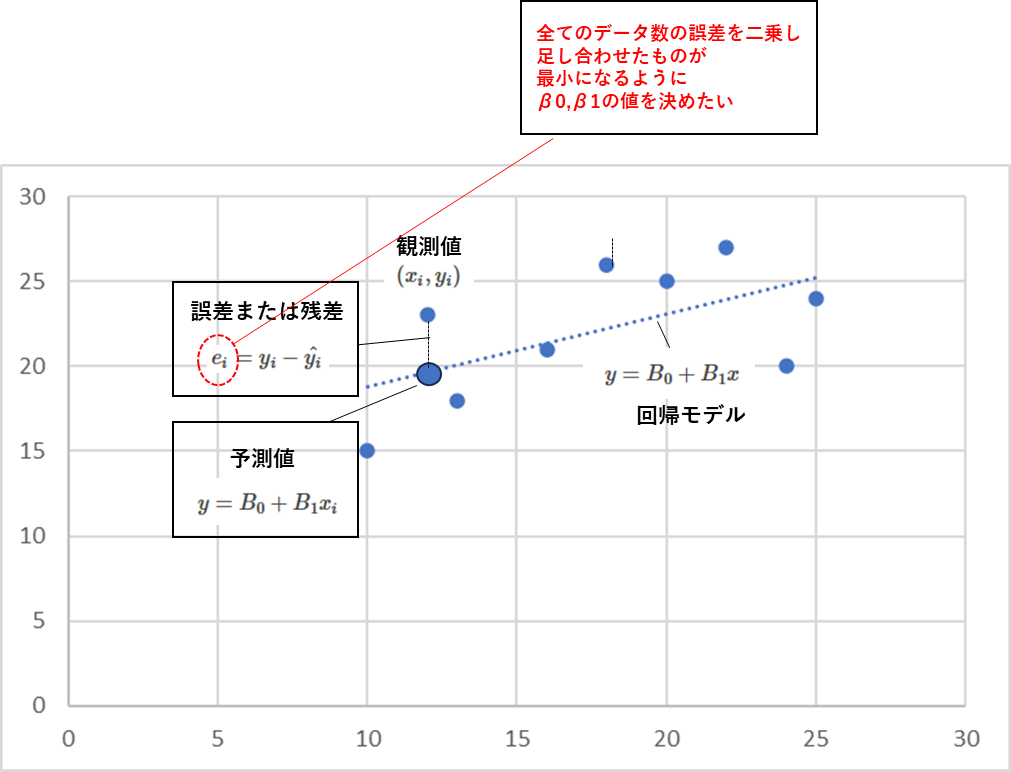
言い換えると
予測値と観測地の誤差の総和が最小になるような
パラメータが良いと考えられます
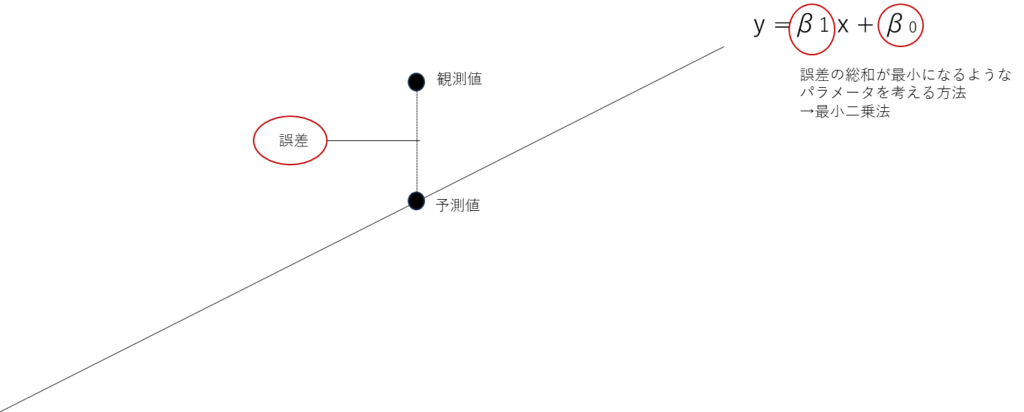
パラメータとは
\(β_0 ,β_1\)
このパラメータを
最小二乗法で求めることを行います
\(\displaystyle S(β_0 , β_1)= \sum_{i=1}^{n}ε_i^2=\sum_{i=1}^{n}(y_i-(β_0 + β_1x_i))^2\)
これは誤差二乗和と呼ばれます
最小二乗法は観測値とモデルの
“予測値との残差(誤差)の二乗和を最小化“
するような回帰係数を求める手法です。

早速最小二乗法
を使って
計算してみよ~
最小二乗法を利用したβ0,β1の推定
最小二乗法を利用して推定された
バラメータは以下になります。
\(B_0=-B_1\bar x+\bar y\)
\(B_1=\displaystyle\frac{S_{xy}}{S_{xx}}\)

式の証明を
していきます
データを用意する
\((x_1,y_1),(x_2,y_2),(x_3,y_3)…..(x_n,y_n)\)

データを
用意しました!
誤差二乗和の式を作る
\(ε_i^2(B_1,B_0)=\displaystyle\sum_{k=1}^{n}(y_i-B_1x_i-B_0)^2\)

このεが最小になるように
すればいいのか~
\(ε(B_1,B_0)\)は
パラメータ\(B_1,B_0\)に関する二次関数です
このεを最小にするには\(B_1,B_0\)で式を偏微分し
0と置いた連立方程式を解くことで
パラメータ\(B_1,B_0\)を解くことが出来る
\(\frac{\partialε(B_1,B_0)}{\partial B_0} =0\)
\(\frac{\partialε(B_1,B_0)}{\partial B_1} =0\)

展開!
\(\frac{\partialε(B_1,B_0)}{\partial B_0} =-2\displaystyle\sum_{k=1}^{n}(y_i-B_1x_i-B_0)=0\)
\(\frac{\partialε(B_1,B_0)}{\partial B_0} =-2\displaystyle\sum_{k=1}^{n}x_i(y_i-B_1x_i-B_0)=0\)
\(B_1\displaystyle \sum_{k=1}^{n}x_i+B_0n=\sum_{k=1}^{n}y_i\) …①
\(B_1\displaystyle \sum_{k=1}^{n}x_i^2+B_0\sum_{k}^{n}x_i=\sum_{k=1}^{n}x_iy_i\)…②
①の式をnで割ると
\(B_1\frac{\sum_{k=1}^{n}x_i}{n}+B_0=\frac{\sum_{k=1}^{n}y_i}{n}\) ・・・(1-1)
- xの平均値
→\(\bar x=\frac{\displaystyle\sum_{k=1}^{n}x_i}{\displaystyle n}\) - yの平均値
→\(\bar y=\frac{\displaystyle\sum_{k=1}^{n}y_i}{\displaystyle n}\) - xの二乗和平均
→\(\bar x^2=\frac{\displaystyle\sum_{k=1}^{n}x_i^2}{\displaystyle n}\) - xとyの積和の平均
→\(\bar{xy}=\frac{\displaystyle\sum_{k=1}^{n}x_iy_i}{\displaystyle n}\)
データの平均の公式を(1-1)に代入すると
\(B_1\bar x +B_0=\bar y\)・・・(1-2)
(1-2)より\(B_0\)は
\(B_0=-B_1\bar x+\bar y\)・・・(1-3)
②の\(B_0\)に(1-3)を代入すると
\(B_1\displaystyle \sum_{k=1}^{n}x_i^2+(-B_1\bar x +\bar y)\sum_{k}^{n}x_i\)
\(\displaystyle=\sum_{k=1}^{n}x_iy_i\)・・・(2-1)
(2-1)を変形してnで割ると
\(B_1(\frac{\sum_{k=1}^{n}x_i^2}{n}-\bar x\frac{\sum_{k=1}^{n}x_i}{n})\)
\(=\frac{\sum_{k=1}^{n}x_iy_i}{n}-\bar y\frac{\sum_{k=1}^{n}x_i}{n}\)・・・(2-2)
(2-2)にデータの平均値の公式を代入すると
\(B_1(\bar x^2-(\bar x)^2)=\bar{xy}-\bar x \bar y\)・・・(2-3)
(2-3)より\(B_1\)は
\(B_1=\displaystyle\frac{\bar{xy}-\bar x \bar y}{\bar x^2-(\bar x)^2}\)・・・(2-4)
\(B_1=\displaystyle\frac{S_{xy}}{S_{xx}}\)
エクセルで回帰係数の計算をしよう

最後にエクセルで
簡単に回帰係数の
計算を
する方法教えちゃいます!
散布図を作り、回帰直線を表示して確認する
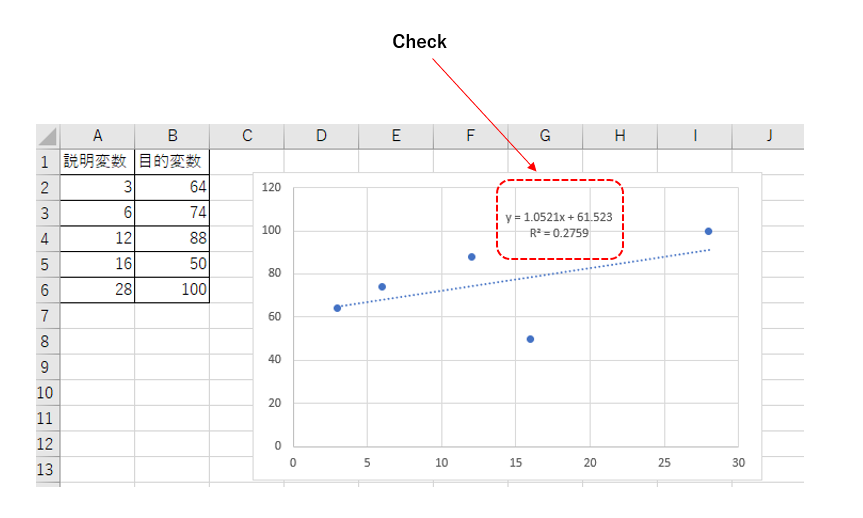
\(B_1=1.0521,B_2=61.523\)であることが確認できる
エクセル統計の回帰分析を利用して回帰係数を求める
データからデータ分析をクリックして回帰分析を選択する
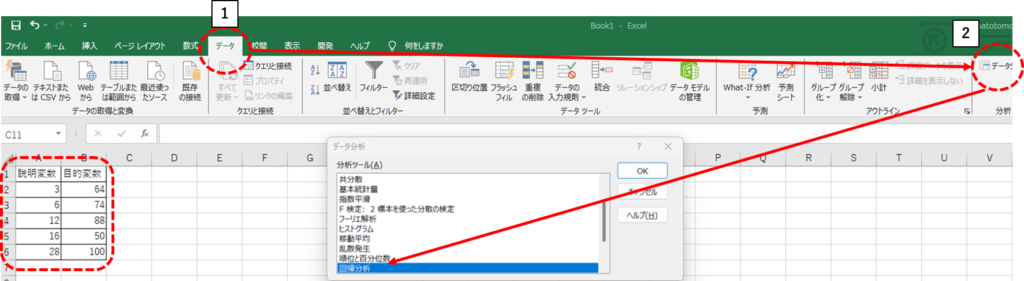
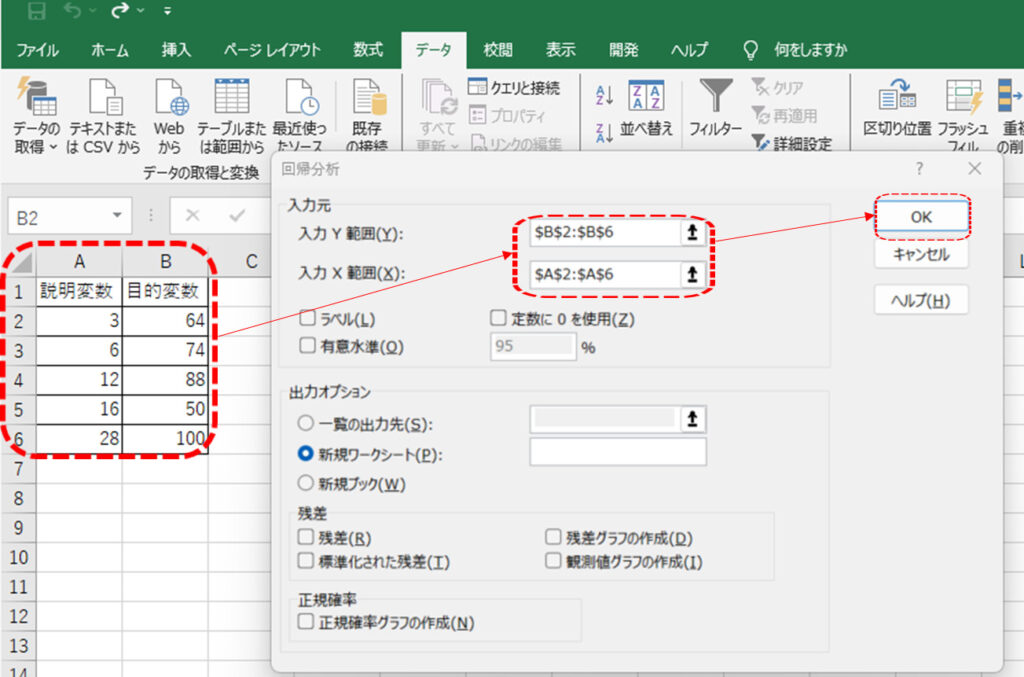
入力範囲Yに目的変数、入力範囲Xに説明変数を入れる
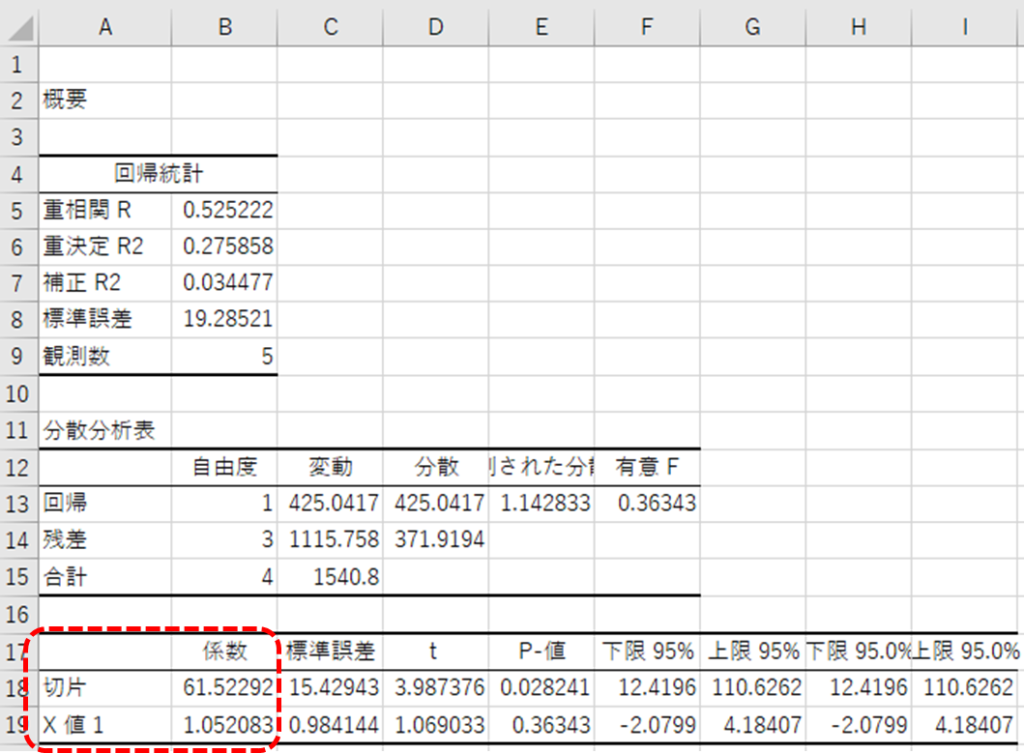
エクセルの係数欄を確認する
目的変数の予測
回帰係数を求めると単回帰直線を作ることが出来る
モデルが出来たので
このモデルを使用して
目的変数の予測をすることが出来る
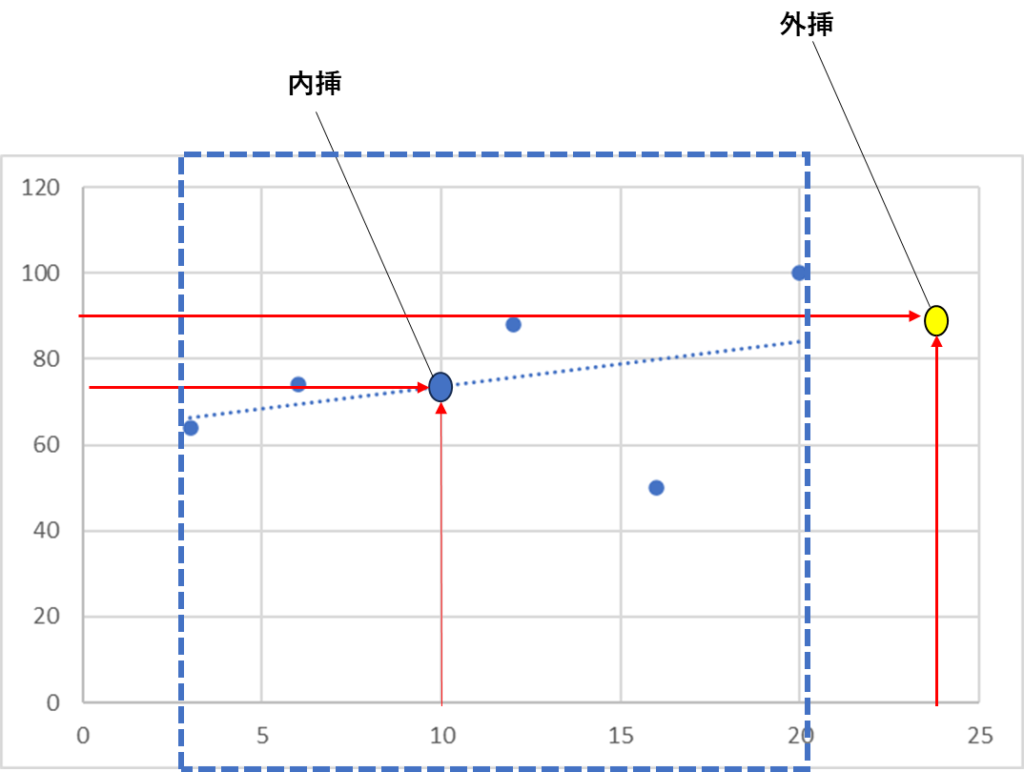
観測値内で予測することを内挿
観測値外で予測することを外挿という
観測値外で予測する時は
モデルからデータが外れている
可能性があるので慎重に判断する必要がある。

予測は慎重にね!
当てはまりの評価
回帰モデルの当てはまり(適合度)を
評価する方法はいくつかあります
代表的な評価指標を簡単に紹介していきます。
平均絶対誤差(MAE – Mean Absolute Error)
各観測値において実際の値と予測値の絶対値の平均を取る
\(MAE=\frac{1}{n}\sum_{k=1}^{n}\left|y_i-\hat y_i\right|\)
小さいほど良いモデルの適合度を示す
平均二乗誤差(MSE – Mean Squared Error)
各観測値において
実際の値と予測値の差の二乗の平均を取ります。
\(MSE=\frac{1}{n}\sum_{k=1}^{n}(y_i-\hat y_i)^2\)
小さいほど良いモデルの適合度を示す
二乗しているため大きな誤差が大きくなる
平均二乗平方根誤差(RMSE – Root Mean Squared Error)
平均二乗誤差の平方根を取ります
\(RMSE=\sqrt{MSE}\)
RMSEも小さいほど適合度が高いとされます
MSEの単位を元に戻したものと考えることができます
決定係数(\(R^2\) – Coefficient of Determination)
モデルによって説明される分散の割合を示します
最大値は1で、1に近いほど適合度が高いとされます
\(R^2=1-\frac{\displaystyle \sum_{k=1}^{n}(y_i-\hat y_i)^2}{\displaystyle \sum_{k=1}^{n}(y_i-\bar y_i)^2}\)
以上が単回帰モデルの回帰係数(パラメータ)の推定
目的変数の推定について解説でした!
ありがとうございました。