標本分散と不偏分散の違いとは?

[PR]※本サイトには、プロモーションが含まれています

標本分散と不偏分散

標本分散と不偏分散は

以下の式で表すことができます

分散	式	エクセル関数
標本分散	\(\displaystyle s^2 =\frac{1}{n}\sum_{i=1}^{n}(x_i-\bar x)^2\)	=VAR.P(:)
不偏分散	\(\displaystyle \hat σ^2 =\frac{1}{n-1}\sum_{i=1}^{n}(x_i-\bar x)^2\)	=VAR.S(:)

標本分散は

標本から計算した分散

不偏分散は

標本から推定された母集団の分散

です。

標本分散

標本から計算した分散です

標本とは?

母集団の部分集合

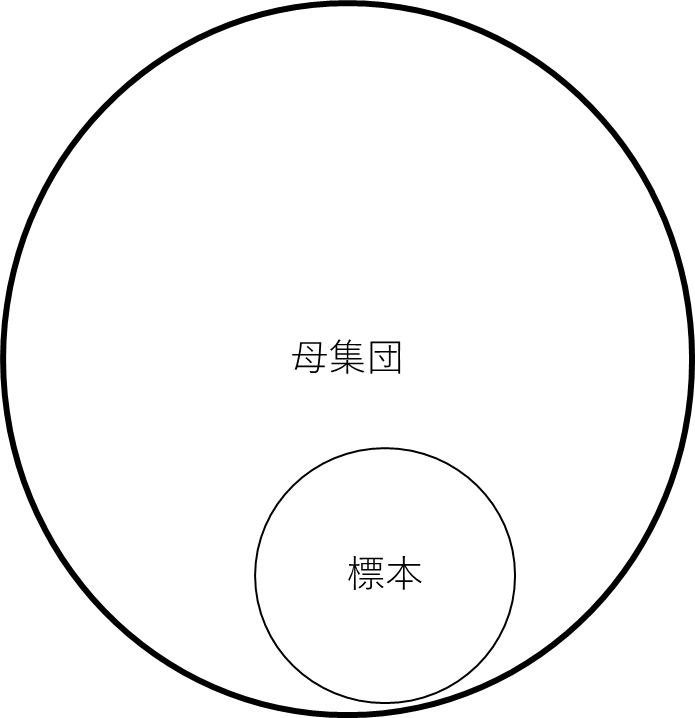
母集団はデータ量,情報が

とてつもなく大きい

すべてを得ることは

限りなく不可能に近いです

そこで我々は母集団から

一部の情報を得ます

一部の情報の事を

標本と言います

例題

1学年100人 , 1クラス20人,計5クラス
の高校がある1クラス2人の数学の点数
を確認すると以下のような点数になった
分散,標準偏差を求めよ

A組	A組	B組	B組	C組	C組	D組	D組	E組	E組
62	58	72	64	45	67	73	53	38	41

標本分散を聞かれているので

\(\displaystyle s^2 =\frac{1}{10}\sum_{i=1}^{n}(x_i-\bar x)^2\)

\(=143.21\)

標準偏差は

\(\displaystyle s =\sqrt{\frac{1}{10}\sum_{i=1}^{n}(x_i-\bar x)^2}\)

\(=11.97\)

8人の数学の点数は12.6点ばらついている

ことが分かりました。

不偏分散

標本から推定された母集団の分散です

簡単に言うと不変分散は

標本を使って母分散を計算した値

ということです

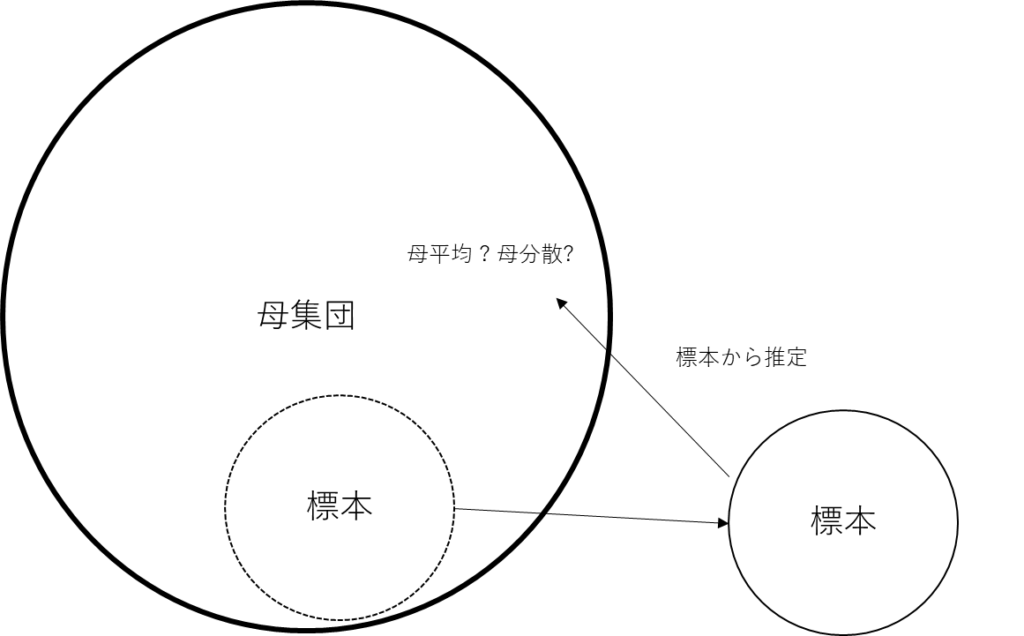
不偏分散を説明するには

点推定を説明する必要があるので

点推定の説明からします

点推定

点推定とは

未知の母数\(θ\)をデータから

推定する作業のことである

推定された値は推定量と

呼ばれ\(θ\)の前にハットをつけて

\(\hat θ\)で表す

推定量\(\hat θ\)が

全ての値に対して

\(E(\hat θ)=θ\)となるとき

\(\hat θ\)を\(θ\)の不偏推定量と呼ぶ

上記のルールから

不偏分散は母分散の不偏推定量

ということが言えます

分散の不偏推定量

では母分散\(σ^2\)の推定量として

そのまま標本分散を使えばいいのでは?

となりますが

\(E(標本分散)=σ^2\)

は成り立たないが

\(E(不偏分散)=σ^2\)

の時は成り立つ

それを証明していきます

偏差平方和から不偏分散の式の証明

偏差平方和\(T_{xx}\)を使って

証明していきます

\(T_{xx} = \sum(x_i-\bar x)^2\)

\(=\sum[(x_i-μ)-(\bar x -μ)]^2\)

\(=\sum(x_i-μ)^2-n(\bar x -μ)^2\)

ここで期待値の計算をすると

\(E[T_{xx}]=\sum E[(x_i-μ)^2]-nE[(\bar x -μ)]^2\)

\(=\sum V[x_i] – nV[\bar x] \)

\(\displaystyle =nσ^2 – n\frac{σ^2}{n}\)

\(=(n-1)σ^2\)

\(\displaystyle E[s^2] =E[\frac{T_{xx}}{n}] = [\frac{n-1}{n}]σ^2 \neq σ\)

\(\displaystyle E[\hat σ^2] =E[\frac{T_{xx}}{n-1}] = [\frac{n-1}{n-1}]σ^2 = σ\)

\(\displaystyle \hat σ^2 = \frac{T_{xx}}{n-1}\)

\(\displaystyle \hat σ^2 =\frac{1}{n-1}\sum_{i=1}^{n}(x_i-\bar x)^2\)

参考文献

Bitly

amzn.to