
今回は単回帰モデルのパラメータ
推定方法 最尤法の考え方に
ついて理解していきたいと思います
[PR]※本サイトにはプロモーションが含まれています
回帰直線とは?
データから
2つの変数の関係性を
直線関係として推定
モデル化したものです
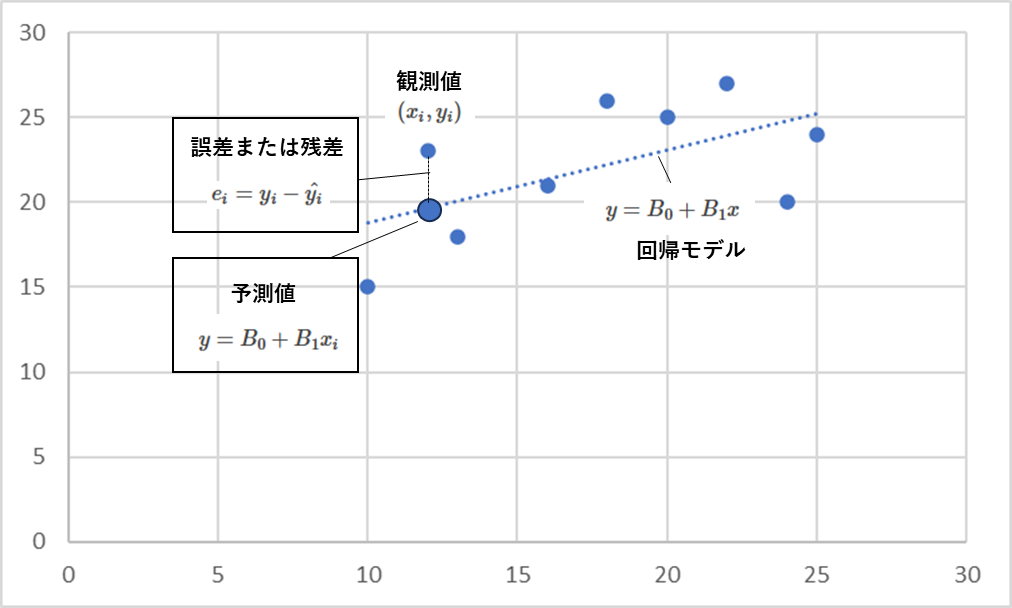
最尤法は2つのパラメータ\(B_0 , B_1\)
を推定する手法です
最尤法の考え方
線形単回帰モデルの式を観察します
\(y_i = β_0 + β_1x_i + ε_i\)
iは観測データの番号で
\(ε_i\)は各iで平均0,分散 \(σ^2\)の正規分布の元で発生する
確率変数と仮定します
\(\displaystyle f(x) = \frac{1}{\sqrt{2πσ^2}}exp(-\frac{x^2}{2σ^2})\)
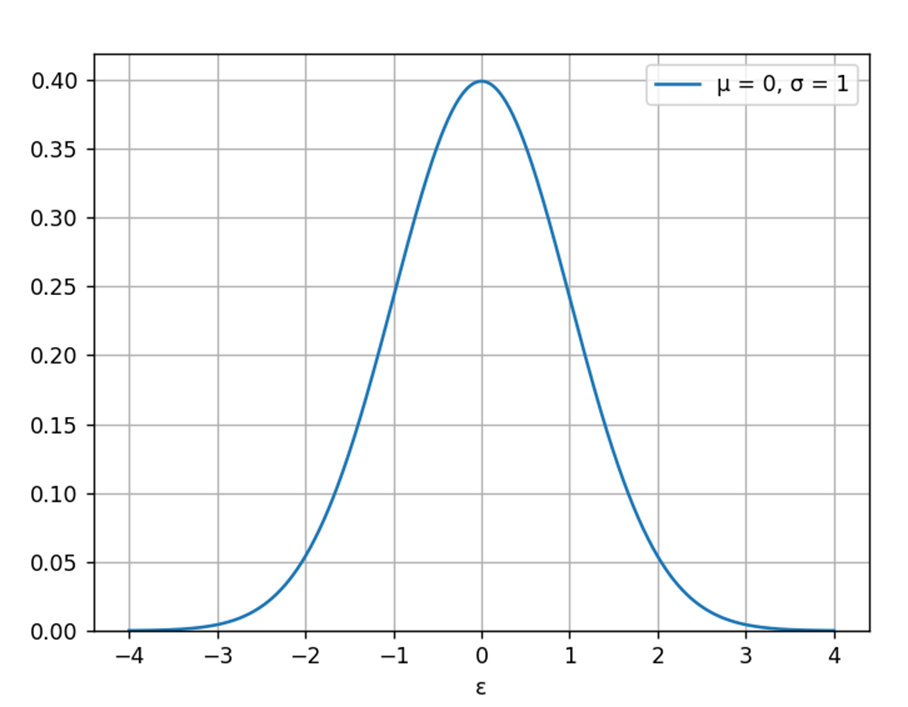

誤差は上の分布の元で
発生すると考えているから
-4から4のレンジのどれか
の値をとるって
感じだね
この時観測値\(y_i\)は
平均\(β_0 + β_1x_i\),
分散\(σ^2\)の正規分布に従います
\(\displaystyle f(y_i❘ x_i;β_0,β_1) = \frac{1}{\sqrt{2πσ^2}}exp(-\frac{[y-(β_0 + β_1x_i)]^2}{2σ^2})\)
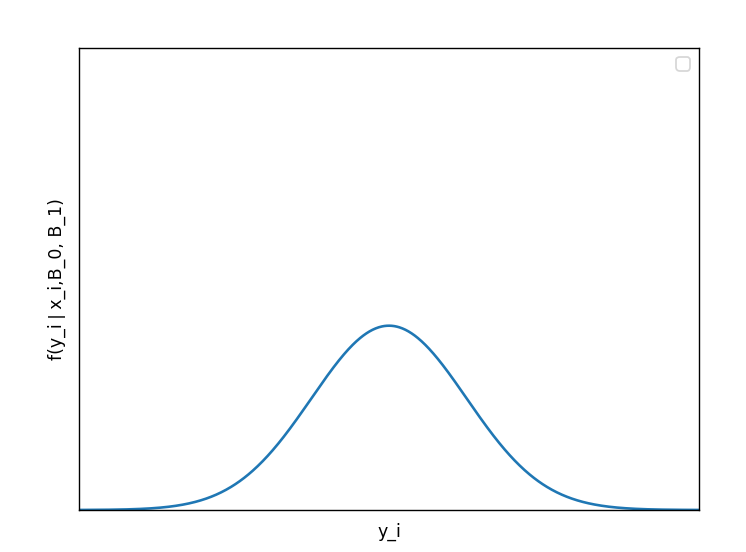
\(y_i\)は\(β_0 + β_1\)から誤差\(ε_i\)の分だけずれることがわかる
データ数を1~nとし
確率密度関数のデータ全て掛け合わすと
\(L(β_0, β_1, σ^2)\)
\( = f(y_1❘ x_1;β_0,β_1)× ・・・×f(y_n❘x_n;β_0,β_1)\)
\(L(β_0, β_1, σ^2) \)を最尤関数と呼びます
実データと回帰直線の当てはまりが良い場合
\(β_0 + β_1x_i\)の値が\(y_i\)に近いということなので
\(L(β_0, β_1, σ^2) \)が大きくなります
最尤法ではこの最尤関数を最大化するパラメータを推定量とします
実際には対数最尤関数を最大化する問題と考える
\(\displaystyle logL(β_0, β_1, σ^2)\)
\(= -\frac{n}{2}log(2πσ^2)-\frac{1}{2σ^2}\sum_{i =1}^{n}[y_i-(β_0 +β_1x_i)]^2\)
この式が最大となる\(β_0,β_1\)を求めることで
バラメータが取得できます
単回帰モデルの回帰係数\(β_0, β_1\)の
最尤推定量は最小二乗法と一致します

最尤法と最小二乗法で
単回帰のパラメータを推定した時
最終的には
一緒になるんだね
参考文献


第2章 最尤法


