あい
今回はエクセルで
データから
回帰直線を
作っていきます
[PR]※本サイトにはプロモーションが含まれています
合わせて読みたい
目次
回帰分析とは?
回帰分析は
データから数式を作って
2つ以上の変数間の関係性を
モデル化しモデルから目的変数を
理解、予測するために
用いられる統計的手法です。
単回帰分析とは?
単回帰分析は
1つの説明変数と1つ目的関数
の関係性を直線でモデル化し
目的変数を理解、予測する
統計的手法です
単回帰直線の数学モデル
単回帰分析の数学モデル
\(y=B_0+B_1x+ε\)
yは目的変数、x は説明変数
β0 は切片(y軸との交点)
β1 は回帰係数、ε は誤差

あい
早速データから
回帰直線を
作っていきます!
データから回帰直線を作る
例題
ある工場で、ある材料を製造しているが製品の特性値yと
焼成温度xの関係性を調べる必要が生じた下記のような
データからxとyの関係性を解析せよ
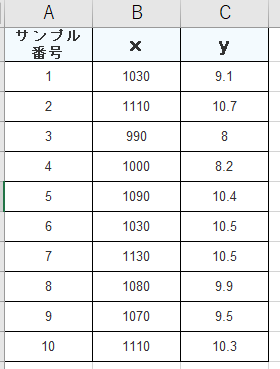
| サンプル番号 | x | y |
| 1 | 1030 | 9.1 |
| 2 | 1110 | 10.7 |
| 3 | 990 | 8 |
| 4 | 1000 | 8.2 |
| 5 | 1090 | 10.4 |
| 6 | 1030 | 10.5 |
| 7 | 1130 | 10.5 |
| 8 | 1080 | 9.9 |
| 9 | 1070 | 9.5 |
| 10 | 1110 | 10.3 |

あい
2つのデータの
関係を見るために
散布図
エクセルで
描きます
データをセットする

あい
エクセルに
データを
セットします
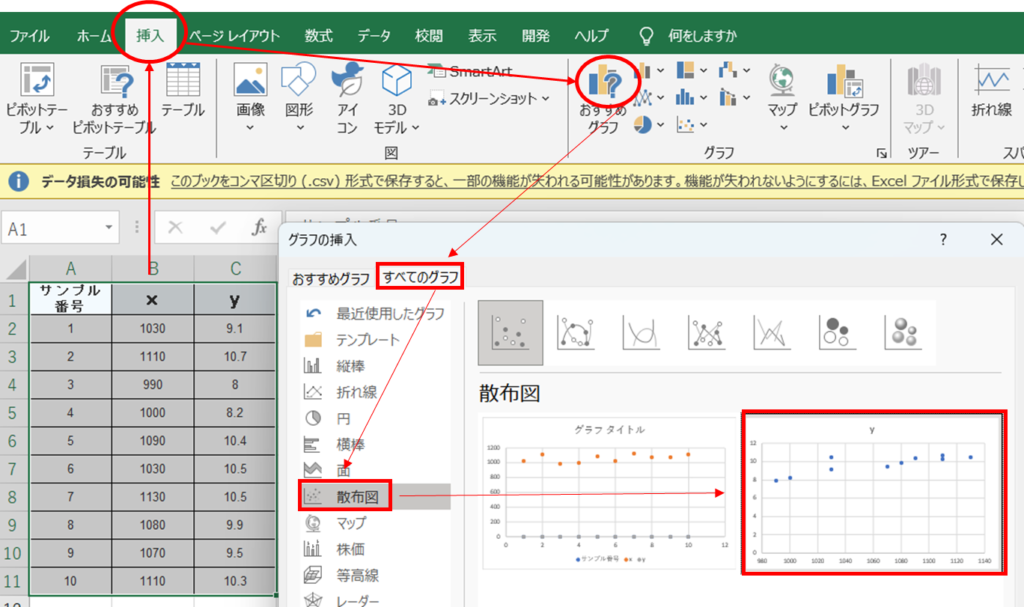
挿入からグラフを作る

あい
散布図を作る
一連の動作です

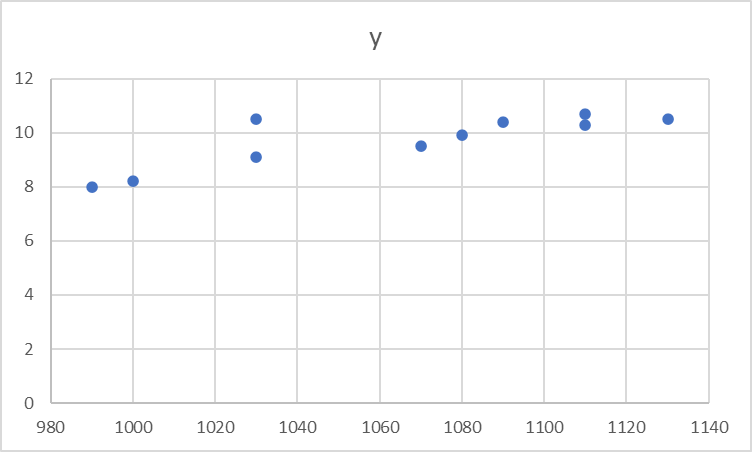
あい
でてくるものが
こちらになります

あい
グラフタイトル
軸のスケール
縦軸、横軸のラベル
メモリのスケール
を調整しました
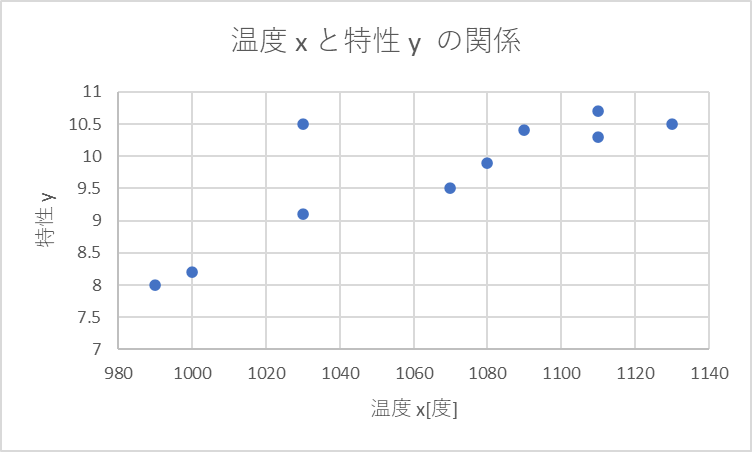

あい
xとyの関係性を
見ると温度xが
高くなると
特性yが
増加している
ように見えます
グラフ要素から近似曲線を選択する
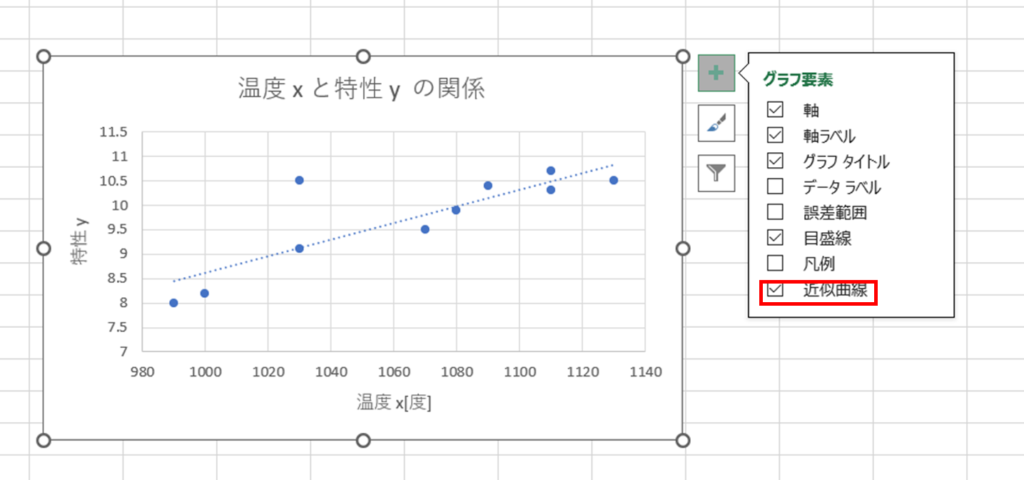

あい
直線が引けました
次に直線の
数式を考えて
いきます
単回帰直線に数式を挿入する
直線を右クリックし
近似直線の書式設定(E)を
押した後グラフに数式を表示する
にチェックを入れます
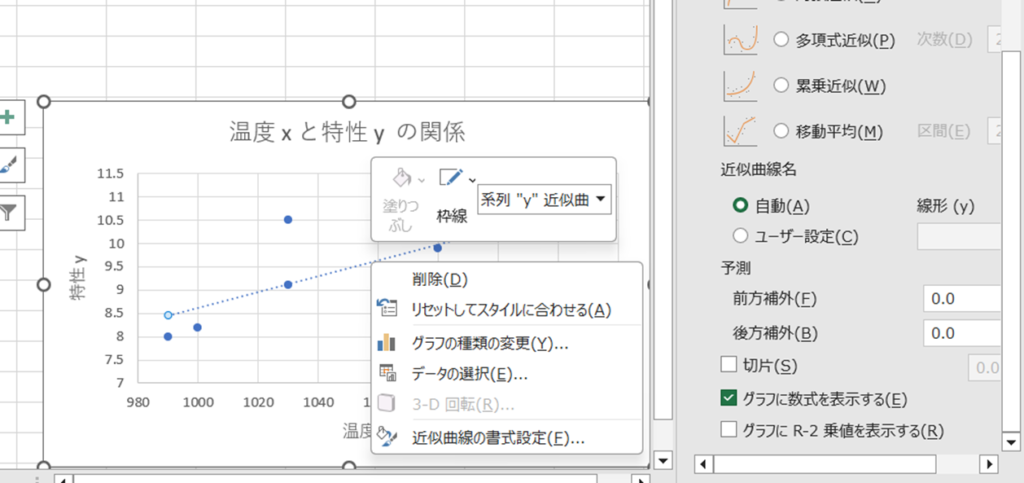
出来ました。
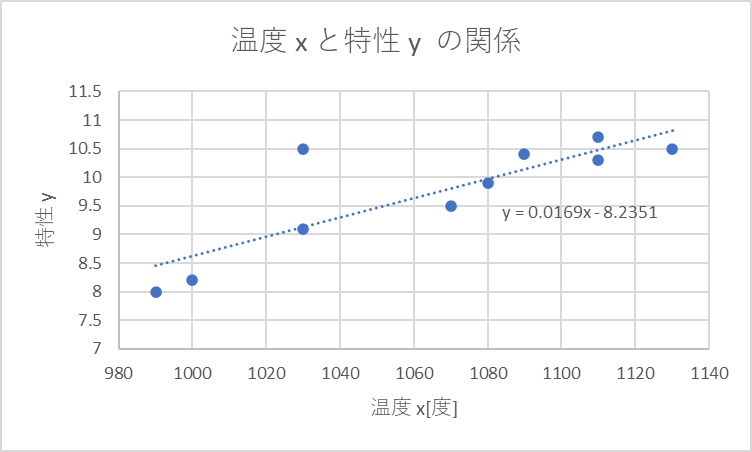
\(y = 0.0169 x -8.2351\)
といった答えが出ましたねこれで数式化完了です
\( x = 1000\)と入れたら\(y = 8.66\)
になります。
温度が1000度だったら特性値は8.66に
なるよといった数式ができました
予測値と残差
回帰直線を利用して推定された値が予測値
実際の値と予測値の差を残差といいます
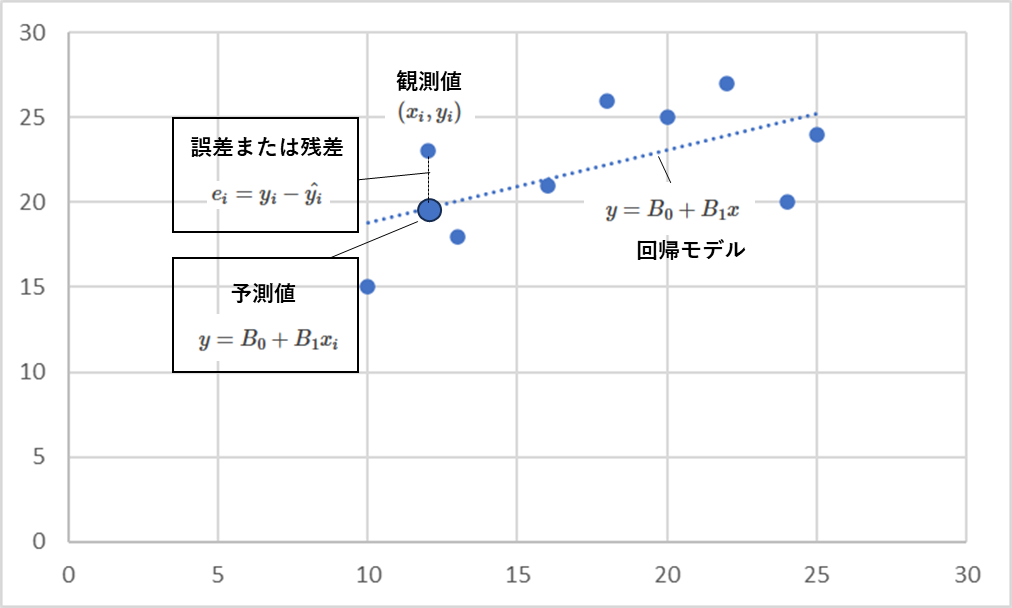
線形単回帰モデルの例
- 薬物の投与量xに対し、期待される効果yの影響の大きさ
- 最寄りの駅の乗降者数xじゃお店の売上高yにどれくらいの影響を与えているか
- 最寄りの駅からの距離xはお店の売上高にどれくらいの影響を与えているのか
回帰分析における基本用語
| 用語 | 用語説明 |
| 説明変数 | 指定できる変数 |
| 目的変数 | この値を 他の変数によってコントロールすることが 目的なので目的変数という |
| 予測値 | 回帰直線を利用して推定されたyの値 |
| 残差 | 目的変数と予測値の差 |