色々なデータをロジスティック回帰モデルに当てはめてみる

Yamu

今回は2つのデータセットに
ロジスティック回帰モデルに
当てはめてグラフを観察します

[PR]※本サイトにはプロモーションが含まれています

合わせて読みたい

【回帰分析】ロジスティック回帰モデルとは ?糖尿病の疾患と血糖値のデータでモデル化して説明する

Rを使ってロジスティック回帰を実装する

1 今回使用するデータセット
2 ロジスティック回帰モデル
3 モデルの評価
- 3.1 残差逸脱度

今回使用するデータセット

1.殺虫剤の濃度と死亡率

殺虫剤の濃度 x	0.4	0.57	0.7	0.8	1
虫の数	51	48	46	49	50
死亡数	6	16	24	42	44
死亡率	0.12	0.33	0.522	0.857	0.88

表1 :殺虫剤の濃度と死亡率

下記コードでpythonにデータセットしておきます

import pandas as pd

# データの定義
data1 = {
    '殺虫剤の強さ': [0.4, 0.57, 0.7, 0.8, 1],
    '虫の数': [51, 48, 46, 49, 50],
    '死亡数': [6, 16, 24, 42, 44],
    '死亡率': [0.12, 0.33, 0.522, 0.857, 0.88]
}

# データフレームの作成
df1 = pd.DataFrame(data1)

# データフレームの表示
print(df1)

   殺虫剤の強さ  虫の数  死亡数    死亡率
0    0.40   51    6  0.120
1    0.57   48   16  0.330
2    0.70   46   24  0.522
3    0.80   49   42  0.857
4    1.00   50   44  0.880

2.肺疾患と喫煙データ

喫煙本数 x	2	6	6	10	14	19	22	27
肺疾患の有無 y	0	0	0	0	1	0	1	1

表2 :殺虫剤の濃度と死亡率

下記コードでpythonにデータセットしておきます

import pandas as pd

# データの定義
data2 = {
    '喫煙本数': [2, 6, 6, 10, 14, 19, 22, 27],
    '肺疾患の有無': [0, 0, 0, 0, 1, 0, 1, 1]
}

# データフレームの作成
df2 = pd.DataFrame(data2)

# データフレームの表示
print(df2)

   喫煙本数  肺疾患の有無
0     2       0
1     6       0
2     6       0
3    10       0
4    14       1
5    19       0
6    22       1
7    27       1

ロジスティック回帰モデル

2つのデータセットに

ロジスティック回帰モデルを適応してみる

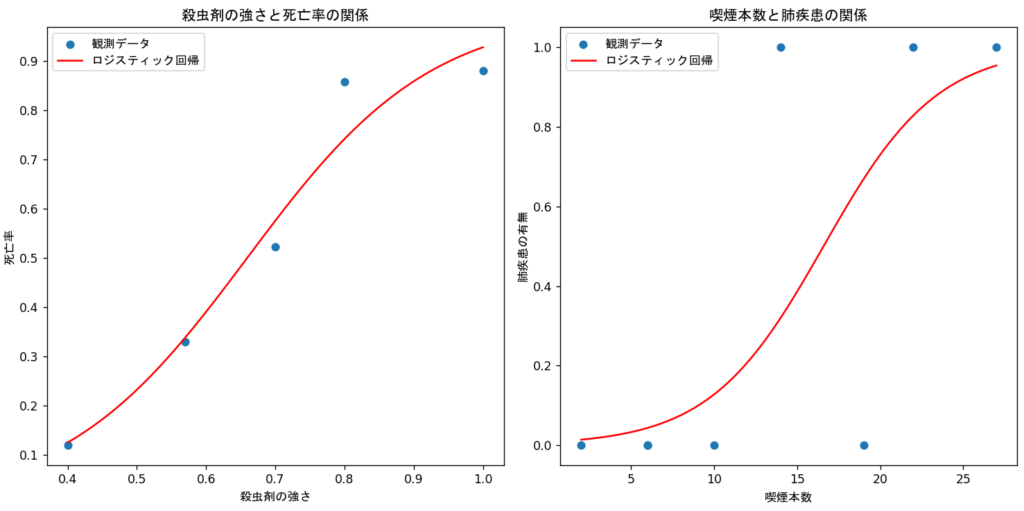
殺虫剤と死亡率のデータに対し

ロジスティック回帰モデルは

当てはまっているように見える

肺疾患の有無のデータでは

煙草の本数が増えるほど

肺疾患を持っている人が確認できているので

1日に何本吸ったら肺疾患になる確率は

何%といった診断ができるかもしれません

下記のコードでデータから

ロジスティック回帰モデルを実装しました

import pandas as pd
import statsmodels.api as sm
import numpy as np
import matplotlib.pyplot as plt

# データの定義
data1 = {
    '殺虫剤の強さ': [0.4, 0.57, 0.7, 0.8, 1],
    '虫の数': [51, 48, 46, 49, 50],
    '死亡数': [6, 16, 24, 42, 44],
    '死亡率': [0.12, 0.33, 0.522, 0.857, 0.88]
}

data2 = {
    '喫煙本数': [2, 6, 6, 10, 14, 19, 22, 27],
    '肺疾患の有無': [0, 0, 0, 0, 1, 0, 1, 1]
}

# データフレームの作成
df1 = pd.DataFrame(data1)
df2 = pd.DataFrame(data2)

# グラフの設定
fig, axs = plt.subplots(1, 2, figsize=(12, 6))

# 日本語フォントの設定
plt.rcParams['font.family'] = 'MS Gothic'

# 1つ目のグラフ: 殺虫剤の強さと死亡率
# ロジスティック回帰モデルの作成
X1 = sm.add_constant(df1['殺虫剤の強さ'])  # 切片項を追加
y1 = df1['死亡率']
logit_model1 = sm.Logit(y1, X1)
result1 = logit_model1.fit()

# 殺虫剤の強さの範囲で予測を行う
X_pred1 = np.linspace(df1['殺虫剤の強さ'].min(), df1['殺虫剤の強さ'].max(), 100)
X_pred1 = sm.add_constant(X_pred1)
y_pred1 = result1.predict(X_pred1)

# 散布図と予測結果のプロット
axs[0].scatter(df1['殺虫剤の強さ'], df1['死亡率'], label='観測データ')
axs[0].plot(X_pred1[:, 1], y_pred1, color='red', label='ロジスティック回帰')
axs[0].set_xlabel('殺虫剤の強さ', fontname="MS Gothic")
axs[0].set_ylabel('死亡率', fontname="MS Gothic")
axs[0].set_title('殺虫剤の強さと死亡率の関係', fontname="MS Gothic")
axs[0].legend()

# 2つ目のグラフ: 喫煙本数と肺疾患の有無
# ロジスティック回帰モデルの作成
X2 = sm.add_constant(df2['喫煙本数'])  # 切片項を追加
y2 = df2['肺疾患の有無']
logit_model2 = sm.Logit(y2, X2)
result2 = logit_model2.fit()

# 喫煙本数の範囲で予測を行う
X_pred2 = np.linspace(df2['喫煙本数'].min(), df2['喫煙本数'].max(), 100)
X_pred2 = sm.add_constant(X_pred2)
y_pred2 = result2.predict(X_pred2)

# 散布図と予測結果のプロット
axs[1].scatter(df2['喫煙本数'], df2['肺疾患の有無'], label='観測データ')
axs[1].plot(X_pred2[:, 1], y_pred2, color='red', label='ロジスティック回帰')
axs[1].set_xlabel('喫煙本数', fontname="MS Gothic")
axs[1].set_ylabel('肺疾患の有無', fontname="MS Gothic")
axs[1].set_title('喫煙本数と肺疾患の関係', fontname="MS Gothic")
axs[1].legend()

# グラフの表示
plt.tight_layout()
plt.show()