偏差,平方和,分散,標準偏差を理解する

合わせて読みたい	概要
平均値,トリム平均,中央値,最頻値を理解する	平均値,トリム平均,中央値,最頻値について分かりやすく説明しています
標本分散と不偏分散の違いとは?	標本分散と不偏分散の違いに注目した記事です

[PR]※本サイトには、プロモーションが含まれています

今回説明する統計量 !

統計量	公式
偏差	\(\displaystyle x_n-\overline x\)
平方和	\(\displaystyle \sum_{k=1}^{n}(x_k-\overline x)^2\)
分散	\(\displaystyle \frac{1}{n}\sum_{k=1}^{n}(x_k-\overline x)^2\)
標準偏差	\(\displaystyle \sqrt{\frac{1}{n}\sum_{k=1}^{n}(x_k-\overline x)^2}\)

散布度

散布度とは

データの散らばり具合を示す値です。

3人の国語の点数データがあります。

科目	A君	B君	C君
国語	60	70	75

同じ国語のテストを受けても

点数が60点,70点,75点と

人によってバラバラです

このバラバラ具合を数値で示そう

としたものが散布度です

偏差

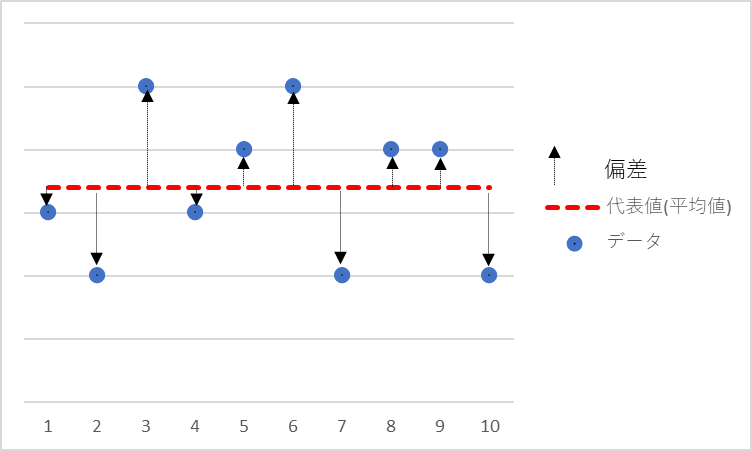
偏差とは

データ 　ー　平均値で

\(\displaystyle x_n-\overline x\)

で表すことが出来ます

平均の値からどれだけ離れているか

を確認する統計量です。

　　　　　　　　　　　　　

偏差の性質

証明

\(\displaystyle\overline x=\frac{(x_1+x_2+x_3…x_n)}{n}\)

\(\displaystyle\sum_{k=1}^{n}(x_k-\overline x)=(x_1+x_2+x_3…+x_n)-n\times\overline x\)

\(=(x_1+x_2+x_3…+x_n)-\displaystyle n\times\frac{(x_1+x_2+x_3…x_n)}{n}\)

\(=0\)

平均偏差

平均偏差は

偏差の絶対値の合計値をデータ数で割ったもの

偏差の総和は0になるが

偏差を絶対値に変換することによって

偏差の問題を解消しています。

偏差平方和(Sum of squares)

偏差平方和は

偏差を二乗した合計

式の展開

\(=\displaystyle \sum_{k=1}^{n}x^2_k-2\overline x \sum_{k=1}^{n}x_k+\overline x^2\)

\(\displaystyle \overline x =\frac{\displaystyle\sum_{k=1}^{n}x_k}{n}\)を代入すると

\(\displaystyle \sum_{k=1}^{n}x_k^2-\frac{\displaystyle(\sum_{k=1}^{n}x_k)^2}{n}\)

分散（variance)

分散とは

「偏差の二乗の総和」÷「データ数 or データ数ー１」

分散は主に標本分散と不偏分散の2種類がある

下記の表にまとめる。

統計量	式
標本分散	\(s^2=\frac{S}{n}\)
不偏分散	\({\hat{σ}}^2=\frac{S}{n-1}\)

標準偏差

標準偏差は

\(s=\sqrt{分散}\)

分散の単位はデータを2乗しているので

測定単位の二乗

になってしまう

この問題解決するため

平方根を利用することで

測定単位を揃えた統計量

として扱うことが出来ます。