平均値,トリム平均,中央値,最頻値を理解する

[PR]※本サイトには、プロモーションが含まれています

今回紹介する統計量

統計量	数学記号	公式	説明
平均(mean)	\(\overline x\)	\(\displaystyle\overline x=\frac{1}{n} \sum_{k=1}^{n}x_k\)	データの中心的な位置を表す
トリム平均	\(\overline x_a\)	\(\displaystyle\overline x=\frac{1}{n-2k} \sum_{i = k +1}^{n-k}x_k\)	外れ値を除いた平均値
中央値(median)	\(median\)	–	データの真ん中の値
最頻値(mode)	\(mode\)	–	出現回数が一番多い値
範囲(range)	\(range\)	\(x_{max} – x_{min}\)	データ範囲

統計量って?

統計量とは

“あるグループのデータの特徴を数値で表したもの“です

統計量はデータの評価をするのに便利な指標です

指標の利便性を説明するために

統計量の一つである平均値を例に説明します

クラスのテストの点数がどちらが上か統計量(平均値)を使って評価する

A組、B組のテストの点数データを用意します

どっちのクラスの方が点数が良いか考えてみる

A組	B組
60	70
45	30
85	55
55	80
60	75

どっちのクラスの方が点数が良いか

表だけでは判断できません

平均値はデータの中心的な位置を表す

よって平均値を利用することで

どっちのクラスの点数が良いか判断していこうと思います

平均値を使ってどちらのクラスの点数が良いか判断する

A組のテストの点数の合計値を

データの総数で割り平均値を算出する

クラスAの平均値を　\(x_A\)と表す

\(\displaystyle\overline x_A =\frac{60+45+85+55+60}{5} = 61\)

B組のテストの点数の合計値を

データの総数で割り平均値を算出する

クラスBの平均値を\(x_B\)と表す

\(\displaystyle\overline x_B =\frac{70+30+55+80+75}{5} = 62\)

1点差でB組の方が高いことが確認できます

このように統計量の一つ平均値を

計算することでグループの特徴を

表し評価することができました

平均値(Mean)

平均値は

“データの合計をデータの総数で割った値“

次にいろいろな平均値の派生形を

紹介します

母平均と標本平均

母平均 :「全体の集団(母集団)の平均」

標本平均: 「サンプリングされたデータの平均」を示す。

平均値の弱点を説明します

平均値は外れ値に弱い

平均値は極端に離れた値

異常値や外れ値に弱い

具体的にデータで説明します

平均値 \(\overline x_1=38.1\) \(\overline x_2=233.8\)

結果から分かるように平均値は

極端な数字に左右されやすいことが分かります

このように外れ値や異常値に対して敏感な統計量は

頑健性(ロバスト性)が低いといいます

それに対してトリム平均は外れ値を除いた平均値なので

頑健性の高い統計量と言えます

頑健性の高いトリム平均について説明します

トリム平均

n個のデータを昇順に並べて

外れ値を取り除いて残りのデータで求めた平均

先ほどの外れ値があるデータ

公式を見ても分かる通り

外れ値を取り除くとき

トリム平均はデータの上下を取り除くルールがある

ので40と2000を取り除きます

トリム平均を計算します

\(\displaystyle\overline x_2 =\frac{40+30+45+53+24+32+38+56}{8} = 39.75\)

中央値(median)

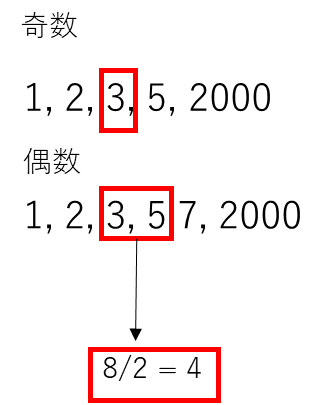
データを昇順に並び替えて

データの個数が奇数の場合は中央に位置する値

偶数の場合は中央の2つの値の平均値

中央値は、外れ値の影響を受けにくい頑健な統計量の1つです

最頻値(mode)

最も多く観測された値

範囲(Range)

データの範囲=最大値-最小値=\(R_{max}-R_{min}\)