
多変量のデータを
一回の処理で散布図にする方法として
散布図行列があります。
今回は散布図行列と
相関行列について解説
pythonで実装する方法を教えます
[PR]※本サイトにはプロモーションが含まれています
目次
散布図行列(Scatter plot matrix)とは
散布図行列は
複数の変数の相関関係を可視化するために使用されるグラフの一種です
散布図行列では
データセット内の複数の変数の内
二変数の相関関係を示す
散布図行列が作成され
各変数の相互関係をみることが出来ます。
データのパターン認識やクラスター
が明らかになり
データの特徴や異常値を見つけるのに役に立つ。
データの型
| 観測番号 | 変数番号1 | 変数番号2 | 変数番号p |
| 1 | \(x_{11}\) | \(x_{12}\) | \(x_{1p}\) |
| 2 | \(x_{21}\) | \(x_{22}\) | \(x_{2p}\) |
| n | \(x_{n1}\) | \(x_{n2}\) | \(x_{np}\) |
散布図行列はp × pで作成されます

早速作ってこー!
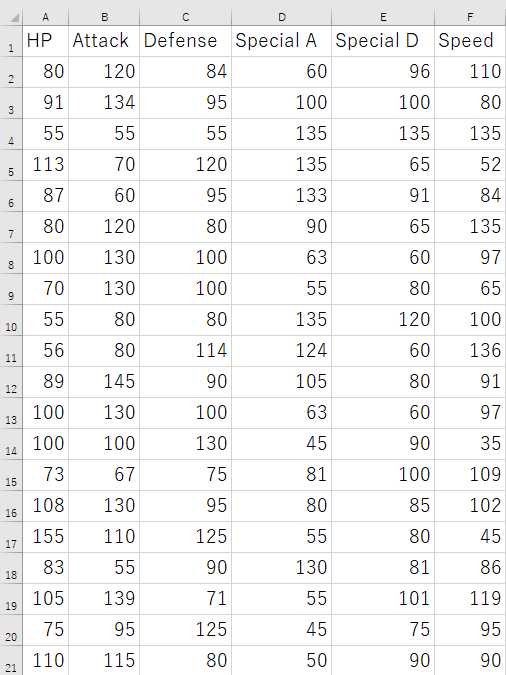
データ準備

ポケモンSVレート対戦のシーズン11,
10/1~11/1の上位ポケモン30の
種族値のデータを持ってきました。
ポケモン使用率ランキング(シーズン11・シングル) | ポケモンバトルデータベース スカーレット・バイオレット (pokedb.tokyo)
| 順位 | ポケモン名 | 種族値合計 | HP | こうげき | ぼうぎょ | とくこう | とくぼう | すばやさ |
| 1 | オーガポン | 550 | 80 | 120 | 84 | 60 | 96 | 110 |
| 2 | カイリュー | 600 | 91 | 134 | 95 | 100 | 100 | 80 |
| 3 | ハバタクカミ | 570 | 55 | 55 | 55 | 135 | 135 | 135 |
| 4 | ガチグマ | 555 | 113 | 70 | 120 | 135 | 65 | 52 |
| 5 | サーフゴー | 550 | 87 | 60 | 95 | 133 | 91 | 84 |
| 6 | パオジアン | 570 | 80 | 120 | 80 | 90 | 65 | 135 |
| 7 | ウーラオス(水 | 550 | 100 | 130 | 100 | 63 | 60 | 97 |
| 8 | ハッサム | 500 | 70 | 130 | 100 | 55 | 80 | 65 |
| 9 | イーユイ | 570 | 55 | 80 | 80 | 135 | 120 | 100 |
| 10 | テツノツツミ | 570 | 56 | 80 | 114 | 124 | 60 | 136 |
| 11 | ランドロス | 600 | 89 | 145 | 90 | 105 | 80 | 91 |
| 12 | ウーラオス(悪 | 550 | 100 | 130 | 100 | 63 | 60 | 97 |
| 13 | キョジオーン | 500 | 100 | 100 | 130 | 45 | 90 | 35 |
| 14 | キュウコン | 505 | 73 | 67 | 75 | 81 | 100 | 109 |
| 15 | ガブリアス | 600 | 108 | 130 | 95 | 80 | 85 | 102 |
| 16 | ディンルー | 570 | 155 | 110 | 125 | 55 | 80 | 45 |
| 17 | キラフロル | 525 | 83 | 55 | 90 | 130 | 81 | 86 |
| 18 | トドロクツキ | 590 | 105 | 139 | 71 | 55 | 101 | 119 |
| 19 | グライオン | 510 | 75 | 95 | 125 | 45 | 75 | 95 |
| 20 | コノヨザル | 535 | 110 | 115 | 80 | 50 | 90 | 90 |
| 21 | イダイトウ | 530 | 120 | 112 | 65 | 80 | 75 | 78 |
| 22 | ヒードラン | 600 | 91 | 90 | 106 | 130 | 106 | 77 |
| 23 | アーマーガア | 495 | 98 | 87 | 105 | 53 | 85 | 67 |
| 24 | セグレイブ | 600 | 115 | 145 | 92 | 75 | 86 | 87 |
| 25 | エンペルト | 530 | 84 | 86 | 88 | 111 | 101 | 60 |
| 26 | ヘイラッシャ | 530 | 150 | 100 | 115 | 65 | 65 | 35 |
| 27 | ミミッキュ | 476 | 55 | 90 | 80 | 50 | 105 | 96 |
| 28 | ドラパルト | 600 | 88 | 120 | 75 | 100 | 75 | 142 |
| 29 | ロトム | 520 | 50 | 65 | 107 | 105 | 107 | 86 |
| 30 | ゴリランダー | 530 | 100 | 125 | 90 | 60 | 70 | 85 |

今回はポケモンの能力
の2つの数値の関係を
確認したいので
散布図行列にして
各能力の
相関関係を
確認したいと思います
散布図行列を実装する
データを整理してCSVファイルに入れます。
Pythonで実装
#CSVからデータを読み込んで散布図行列を作るためのプログラム
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
data=pd.read_csv('/input/Pokemon3.csv')
#散布図行列を作成
scatter_matrix=pd.plotting.scatter_matrix(data,figsize=(10,10),alpha=0.8)
#タイトルを追加
plt.suptitle("Pokemon ability Scatter Plot Matrix ",fontsize=14)
plt.show()複雑な散布図行列も
#散布図行列を作成
scatter_matrix=pd.plotting.scatter_matrix(data,figsize=(10,10),alpha=0.8)を使えばすぐかけます
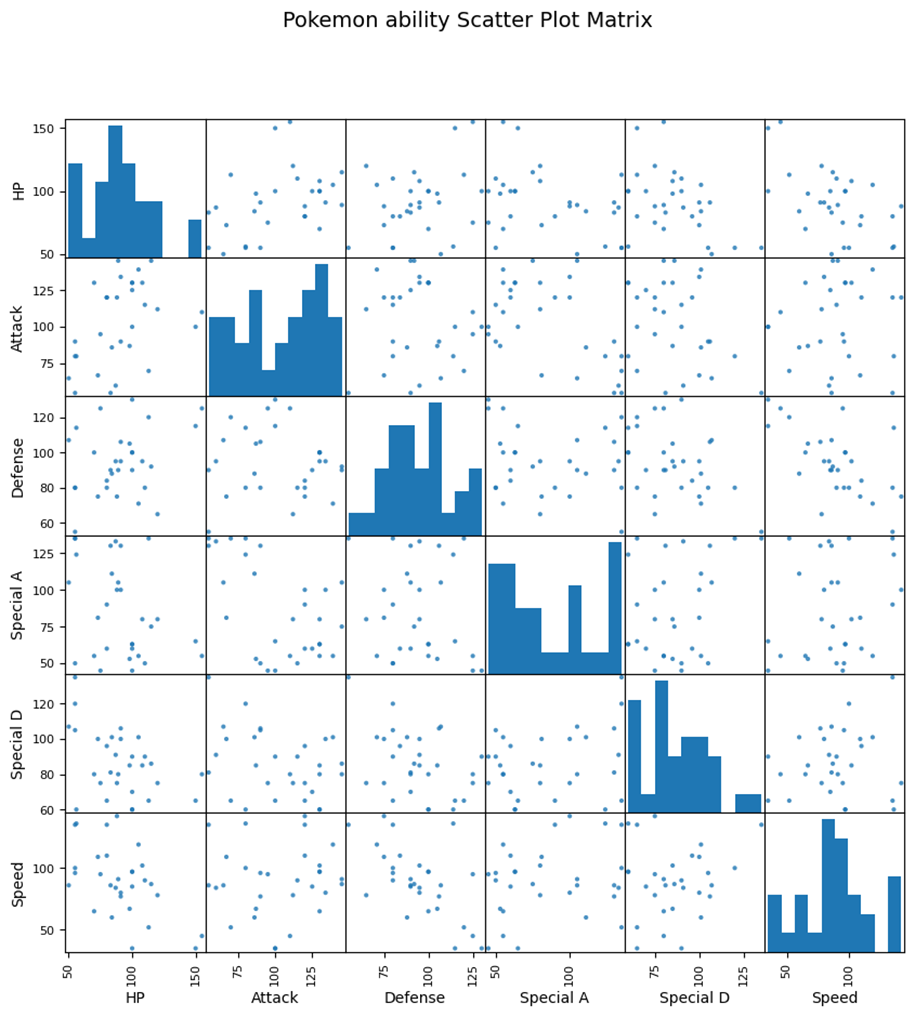

出来た~
相関係数も
グラフに入れてみよう
相関行列(Correlation matrix)
相関行列の要素を見ることで、
互いに相関の強い、弱い変数の組み合わせを
見つけることが出来る。
上記のデータの相関行列計算結果は・・
| HP | こうげき | ぼうぎょ | とくこう | とくぼう | すばやさ | |
| HP | 1 | 0.4 | 0.3 | -0.36 | 0.46 | -0.55 |
| こうげき | 0.4 | 1 | -0.05 | -0.55 | -0.36 | 0.05 |
| ぼうぎょ | 0.3 | -0.05 | 1 | -0.18 | -0.44 | -0.61 |
| とくこう | -0.36 | -0.55 | -0.18 | 1 | 0.28 | 0.22 |
| とくぼう | 0.46 | -0.36 | -0.44 | 0.28 | 1 | 0.12 |
| すばやさ | -0.55 | 0.05 | 0.61 | 0.22 | 0.12 | 1 |
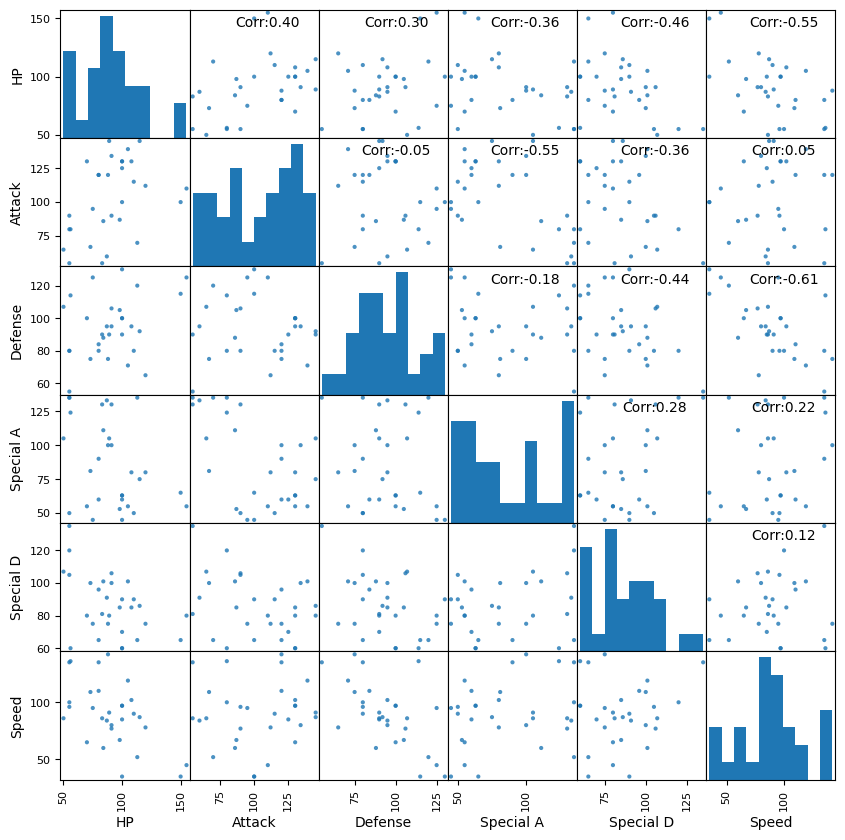
次に上記の相関係数を計算グラフに表記するコードを作成する
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
data=pd.read_csv('/input/Pokemon3.csv')
#相関係数を作成
corr=data.corr()
#散布図行列が計算されているか確認する
#print(corr)
#散布図行列を作成
scatter_matrix=pd.plotting.scatter_matrix(data,figsize=(10,10),alpha=0.8)
plt.suptitle("Pokemon ability Scatter Plot Matrix ",fontsize=14)
#plt.show()
#相関係数を表記
for i,j in zip(*plt.np.triu_indices_from(scatter_matrix,k=1)):
scatter_matrix[i,j].annotate(
f"Corr:{corr.iloc[i,j]:.2f}",
(0.6,0.9),
xycoords='axes fraction',
ha='center',
va='center'
)
plt.show()グラフは・・


出来た~
相関係数も
入ってる!
散布図行列と相関行列から考察してみる
- HPと各変数の相関
→ 体力とこうげき、守備に正の相関がある。
体力ととくこう、とくぼうに負の相関がある。
すばやさ無相関
→シーズン11のトップ30のHPが高いポケモンは攻撃、防御が高く
とくしゅ、とくぼうが低いポケモンが多いのではないか?

HPの多い順に
並び替えて
データを見てみるか
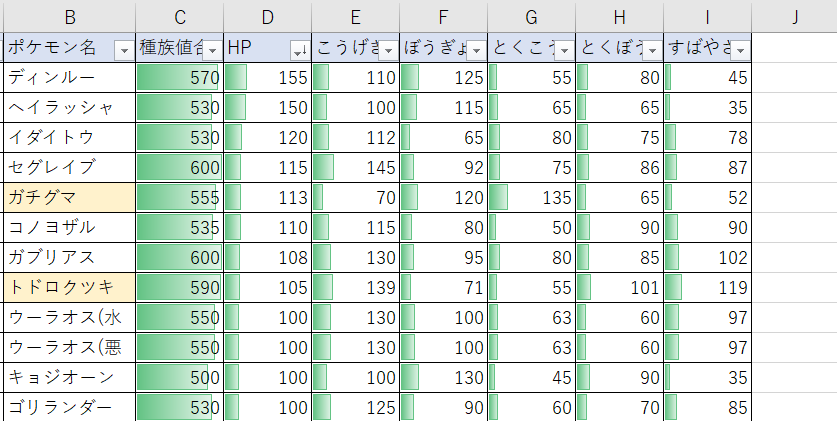

HP Top12のポケモンは
こうげきぼうぎょが100を超えているポケモンが
多くいますが
とくこうとくぼうのどちらかが
100を超えているポケモンは
ガチグマとトドロクツキだけ…
物理アタッカーかつ
防御の高いポケモンがHPTop12に多く
こういうタイプの
ポケモンはとくこう特防が
低い傾向があるのかな…?

